Cantor's Comb

What is Cantor's Comb?

This activity allows the user to step through the process of building Cantor's comb.

The Cantor Comb is a way of visualizing the famous Cantor Set. Start with a line segment like:

Then remove the middle third:

Next, remove the middle thirds of each remaining line segment. The next stage would be:

Now repeat this process indefinitely. The Cantor comb is the stuff left after removing the middle thirds of the line segments "infinitely many times."

Other Cantor combs can be created by removing different sized middle pieces. For example, we can remove the middle quarter (1/4) or the middle half (1/2) to get different Cantor combs. To distinguish between these we sometimes call the original version the "Cantor middle-thirds comb" using a similar name for the others.

Georg Cantor (1845-1918) was very interested in infinite sets, especially ones with unusual properties. He built what is now called the Cantor set to illustrate an unusual infinite set. This set has only points left, no line segments - so no length. If you stop the process at any stage, there are line segments, very short ones. The idea is that at any stage you have length, but in the limit you don't. This makes the Cantor comb a very curious set.

Related Resources

• Activity Another Hilbert Curve Generator
• Discussion about Infinity and Iteration
• Discussion about Recursion
• Discussion about Self-Similarity
• Worksheet Cantor's Comb Exploration Questions
• Worksheet Cantor's Comb Exploration Questions (doc)

How Do I Use This Activity?

This activity allows the user to work step by step through the process of building Cantor's comb.

Controls and Output

• The rectangular area at the top of the applet shows the fractal, which consists of a number of red lines.
• The Previous Step and Next Step buttons move you forward and backward one step in the drawing process.
• This label tells you how long each of the red lines that make up the fractal are (as a fraction of the total width) and what step of the fractal iteration you are on.
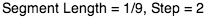
• In the boxes marked Fraction Removed, enter the fraction of each line segment that you want removed at each step. Enter the numerator in the first box and the denominator in the second box. 1/3 is the default. Press the Set button to restart with a new value for Fraction Removed.

Description

This activity allows the user to work step by step through the process of building Cantor's comb. This activity would work well in mixed ability groups of two or three for about thirty to forty-five minutes if you use the exploration questions and ten minutes otherwise.

Place in Mathematics Curriculum

This activity can be used to:

• practice students' fraction manipulation skills
• practice students' pattern finding skills
• demonstrate the complexity of infinity
• motivate the ideas of self-similarity and recursion
• demonstrate fractal objects
• motivate the idea of a limit

Be Prepared to

• work through the first table on the exploration questions with the students
• discuss the concepts of infinity and limit
• review fraction multiplication

Related Resources

• Activity Another Hilbert Curve Generator
• Discussion about Infinity and Iteration
• Discussion about Recursion
• Discussion about Self-Similarity
• Lesson on Introduction to Fractals: Geometric Fractals
• Lesson on Introduction to Fractals: Infinity, Self-Similarity and Recursion
• Lesson on Patterns in Fractals
• Lesson on Properties of Fractals
• Worksheet Cantor's Comb Exploration Questions
• Worksheet Cantor's Comb Exploration Questions (doc)