Fractal Dimensions

What is Fractal Dimensions?

This activity allows the user to calculate the fractal dimension of a series of regular fractals without access to a calculator. It is not necessary to understand logs to use this activity. Calculation of fractal dimension is based upon the fact that Dimension, Scale and Number of similar copies in a geometric fractal follows the formula: 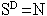For example, the Koch Snowflake 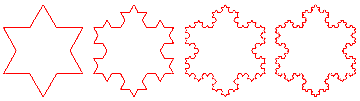is built from replacing a line segment with 4 segments each one third as long as the original, arranged as: The scale factor is 3 and the number of identical copies in the replacement is 4. 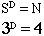Hence, we need to find D so that We can use either trial and error or logarithms to get the answer. In this case the dimension is about 1.262.

How Do I Use This Activity?

This activity allows the user to calculate the fractal dimension of a series of regular fractals without access to a calculator. It is not necessary to understand logarithms to use this activity. This activity shows the user generators for eleven line deformation fractals and two geometric fractals for which the scale factor and the number of copies must be input correctly.

Controls and Output

  • The Next Fractal and Previous Fractal buttons on the left side of the applet control which fractal generator is being viewed.
  • The Enter Scale Factor textfield on the right side of the applet allows you to type in your "guess" for the scale factor for the line deformation you are currently viewing.
  • The Enter Number Of Copies textfield on the right side of the applet allows you to type in your "guess" for the number of copies made from the line deformation you are currently viewing.
  • The Calculate Fractal Dimension button on the right side of the applet will check your guesses from the above textfields.
  • The Result Box below the Calculate Fractal Dimension button will display the result after you have pressed the Calculate Fractal Dimension button.
  • The See a deeper level of this fractal! button on the bottom right side of the applet will become active immediately after you have correctly guessed the scale factor and number of copies for the line deformation you are currently viewing. It allows you to view increasing levels of the line deformation as applied to a straight line.

Scoring

  • This activity will automatically record how successful you are at answering the questions. To view the score, press the Show Score button at the bottom of the activity and a pop-up window will appear with the scoreboard. To close this pop-up window press the Close button or click back on the main window.
  • To pause the scoring, press the Active button at the bottom of the screen and it will change to a Paused button. To resume scoring, press the Paused button.
  • To reset the scoreboard, open the scoreboard using the Show Score button and then press the Reset button.

Description

This activity allows the user to calculate the fractal dimension of a series of regular fractals without access to a calculator. It is not necessary to understand logarithms to use this activity. This activity would work well in same ability groups of two to four for about thirty-five minutes if you use the exploration questions and ten to fifteen minutes otherwise.

Place in Mathematics Curriculum

This activity can be used to:

  • practice students' geometry skills
  • practice students' logarithm skills (optional)
  • illustrate the definition of fractal dimension
  • demonstrate fractal objects

Standards Addressed

Grade 9

  • Geometry

    • The student demonstrates an understanding of geometric relationships.
    • The student solves problems (including real-world situations).
    • The student demonstrates a conceptual understanding of geometric drawings or constructions.

Grade 10

  • Geometry

    • The student demonstrates an understanding of geometric relationships.
    • The student solves problems (including real-world situations).
    • The student demonstrates a conceptual understanding of geometric drawings or constructions.

Number and Quantity

  • Quantities

    • Reason quantitatively and use units to solve problems.

Functions

  • Linear, Quadratic, and Exponential Models

    • Interpret expressions for functions in terms of the situation they model

7th Grade

  • Algebra

    • The student will demonstrate through the mathematical processes an understanding of proportional relationships.

Secondary

  • Algebra II

    • AII.09 The student will find the domain, range, zeros, and inverse of a function; the value of a function for a given element in its domain; and the composition of multiple functions. Functions will include exponential, logarithmic, and those that have domains and ranges that are limited and/or discontinuous. The graphing calculator will be used as a tool to assist in investigation of functions.
    • AII.15 The student will recognize the general shape of polynomial, exponential, and logarithmic functions. The graphing calculator will be used as a tool to investigate the shape and behavior of these functions.
    • AII.9
    • AII.15

Be Prepared to

  • give implicit directions on what they are to do. For example, "Today we are going to fill out the table on the worksheet and see if we can ..."
  • answer the question "How is dimension calculated?"
  • discuss logarithms and exponents