What is The Chaos Game?
This activity allows the user to play the chaos game with a choice of number of vertices.
So why is this game interesting? What happens when we spill out a bag of marbles onto the floor? After they stop rolling around, we get a pattern formed by the marbles - perhaps not a very interesting one. If we spill the same marbles out on the same floor again, do we expect to get the same pattern of marbles? No. The pattern is pretty random, and we expect that. The chaos game was proposed by Michael Barnsley in the mid-1980s as a way to see how patterns can result from certain random events.
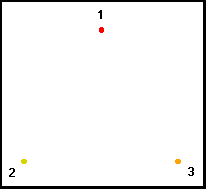
To play the chaos game we start with a set of dots on a page -- we'll call them vertices. The classic game starts with three vertices numbered 1, 2, and 3, and places them at the corners of an equilateral triangle:
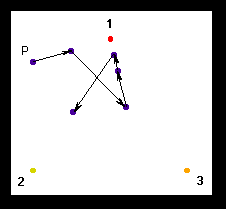
For example, suppose we chose point P below and then rolled a 1, 6, 2, 2, and 4 in that order:
We continue plotting points in this way. After five hundred points a pattern starts to appear:
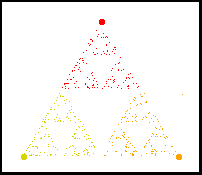
Here we left off the arrows and colored the dots the same as the vertex we moved towards. Recognize the pattern? This is what Barnsley wanted to demonstrate: Randomness can generate a very precise pattern sometimes.
How Do I Use This Activity?
This activity allows the user to see patterns in seemingly random dot arrangements and explore the chaos game by changing the number of vertices, and the number of dots displayed.
Controls and Output
-
The Drawing Area at the top of the applet is where dots are plotted:

You can move the vertices, which appear as larger dots, by clicking and draging with the mouse.
-
Initially, no dots are plotted. To plot some dots, first select the number of dots you
want to add from the
drop-down box, then click the
Add button.
- The Clear button clears all the dots that have been drawn so far.
-
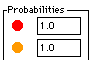
You can choose the
Probability that the game will move towards a certain vertex. The higher the number you type, the
more likely the game is to choose that color. In the example below, red and yellow both
have a probability of 1.0.
-
Besides the probabilities, the
Number of Vertices also affects how the dots are plotted. You can choose the number of vertices by clicking
the
One More or
One Less buttons. You can also select the number of vertices directly from the drop-down box
between those two buttons.

- This version of the Chaos Game is somewhat limited. You can play an Advanced Version by clicking the Go to full version button.
Description
This activity allows the user to play several versions of Barnsley's Chaos Game. This activity would work well in groups of two to four for about thirty-five to forty minutes if you use the exploration questions and fifteen minutes otherwise.
Place in Mathematics Curriculum
This activity can be used to:
- practice students' fraction manipulation skills
- practice students' measurement skills
- practice students' geometric probablility skills
- demonstrate randomness
- motivate the ideas of chaos
- demonstrate fractal objects
Standards Addressed
Grade 6
-
Geometry
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
Grade 7
-
Geometry
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
Grade 8
-
Geometry
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
Grade 9
-
Geometry
- The student demonstrates an understanding of geometric relationships.
- The student demonstrates a conceptual understanding of geometric drawings or constructions.
Grade 10
-
Geometry
- The student demonstrates an understanding of geometric relationships.
- The student demonstrates a conceptual understanding of geometric drawings or constructions.
Geometry
-
Similarity, Right Triangles, and Trigonometry
- Understand similarity in terms of similarity transformations
Grades 9-12
-
Algebra
- Use mathematical models to represent and understand quantitative relationships
-
Data Analysis and Probability
- Develop and evaluate inferences and predictions that are based on data
5th Grade
-
Patterns, Functions, and Algebra
- 5.20 The student will analyze the structure of numerical and geometric patterns (how they change or grow) and express the relationship, using words, tables, graphs, or a mathematical sentence. Concrete materials and calculators will be used.
Be Prepared to
- give implicit directions on what they are to do. For example "Today we are going to see whathappens when we play a random game. Here are the rules ..."
- answer the question "Why/how does this pattern occur?"
- discuss chaos, infinity, etc.