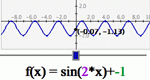Aligned Resources

Introduces students to arithmetic and geometric sequences. Students explore further through producing sequences by varying the starting number, multiplier, and add-on.

Audiences: Grades 6-8, Grades 9-12

Primary Subjects: Algebra, Discrete, Geometry, Number and Operations

Related Topics: addition, arithmetic, arithmetic sequences, geometric sequences, graph, iteration, linear functions, multiplication, multiplier, negative number, pattern, positive number, pre-calculus, recursion, recursive functions, sequences

Students work step-by-step through the generation of a different Hilbert-like Curve (a fractal made from deforming a line by bending it), allowing them to explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: decimals, fractals, fractions, geometric sequences, geometry, iteration, length, pattern, self-similarity, sequences, surface area, symmetry

Enter a set of data points, then derive a function to fit those points. Manipulate the function on a coordinate plane using slider bars. Learn how each constant and coefficient affects the resulting graph.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Algebra, Graphs, Modeling, Statistics, Trigonometry

Related Topics: algebra, cartesian coordinate, coordinate, coordinate plane, coordinate system, cosecant, cosine, cotangent, curve fitting, data plot, deviations, exponential, exponents, function properties, functions, graph, grouping, integers, intervals, inverse, linear equations, linear functions, logarithm, multiplication, parabola, polynomial, positive part of the operand, pre-calculus, range, secant, sine, slope, tangent, trigonometry

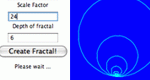
Generate complicated geometric fractals by specifying starting polygon and scale factor.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Geometry

Related Topics: fractals, geometry, logarithm, polygon, recursion, scale, self-similarity

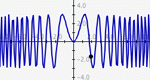
A more advanced version of Slope Slider, this activity allows the manipulation of the constants and coefficients in any function thereby encouraging the user to explore the effects on the graph of the function by changing those numbers.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Algebra, Calculus, Graphs, Trigonometry

Related Topics: algebra, bell curve, calculus, cartesian coordinate, coordinate plane, coordinate system, cosine, decimals, exponential, flyer, function properties, functions, graph, intervals, inverse, linear equations, linear functions, lines, logarithm, parabola, polynomial, pre-calculus, range, sine, slope, tangent, translation, trigonometry

Step through the generation of a Hilbert Curve -- a fractal made from deforming a line by bending it, and explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: chaos, fractals, geometric sequences, geometry, iteration, length, lines, pattern, recursion, self-similarity, sequences

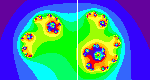
Enter a complex value for "c" in the form of an ordered pair of real numbers. The applet draws the fractal Julia set for that seed value.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: complex number, coordinate plane, coordinate system, fractals, iteration, julia set, mandelbrot set, recursion, recursive functions, sets

Step through the generation of the Koch Snowflake -- a fractal made from deforming the sides of a triangle, and explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: decimals, fractals, geometric sequences, infinity, iteration, lines, pre-calculus, recursion, self-similarity, sequences

Enter a set of data points and a function or multiple functions, then manipulate those functions to fit those points. Manipulate the function on a coordinate plane using slider bars. Learn how each constant and coefficient affects the resulting graph.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Algebra, Calculus, Modeling, Statistics, Trigonometry

Related Topics: algebra, calculus, cartesian coordinate, coordinate, coordinate plane, coordinate system, cosecant, cosine, cotangent, curve fitting, data plot, deviations, flyer, function properties, functions, graph, linear functions, logarithm, parabola, polynomial, pre-calculus, secant, sine, slides, slope, squares, tangent, trigonometry

Graph recursive functions by defining f(0)=C and defining f(n) based on f(n-1).

Audiences: Grades 9-12, Undergraduate

Primary Subjects: Algebra, Discrete, Graphs, Number and Operations

Related Topics: algebra, arithmetic sequences, cartesian coordinate, coordinate plane, functions, geometric sequences, graph, iteration, recursion, recursive functions, sequences

Learn about number patterns in sequences and recursions by specifying a starting number, multiplier, and add-on. The numbers in the sequence are displayed on a graph, and they are also listed below the graph.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Algebra, Discrete, Graphs, Number and Operations

Related Topics: addition, arithmetic, arithmetic sequences, cartesian coordinate, coordinate plane, decimals, geometric sequences, graph, iteration, multiplication, pre-calculus, recursion, recursive functions, sequences

Step through the generation of Sierpinski's Carpet -- a fractal made from subdividing a square into nine smaller squares and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: algebra, area, fractals, fractions, geometric sequences, iteration, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences

Step through the generation of Sierpinski's Triangle -- a fractal made from subdividing a triangle into four smaller triangles and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: dimension, fractals, fractions, geometric sequences, geometry, iteration, length, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences, symmetry, triangle

Explore fractals by investigating the relationships between the Mandelbrot set and Julia sets.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: chaos, complex number, coordinate, coordinate plane, exponents, fractals, functions, geometric sequences, geometry, iteration, julia set, mandelbrot set, pattern, recursion, recursive functions, self-similarity, sets

Enter two complex numbers (z and c) as ordered pairs of real numbers, then click a button to iterate step by step. The iterates are graphed in the x-y plane and printed out in table form. This is an introduction to the idea of prisoners/escapees in iterated functions and the calculation of fractal Julia sets.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Algebra, Geometry, Graphs, Number and Operations

Related Topics: complex number, coordinate plane, coordinate system, exponents, fractals, functions, graph, infinity, iteration, julia set, mandelbrot set, recursion, recursive functions, sets