Aligned Resources

Introduces students to the ideas involved in understanding fractals.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: area, distance, fractals, fractions, generator, geometric sequences, geometry, infinity, initiator, iteration, length, limit, lines, multiplication, pattern, percents, perimeter, recursion, scale, segment, self-similarity, sequences, sets

Introduces students to arithmetic and geometric sequences. Students explore further through producing sequences by varying the starting number, multiplier, and add-on.

Audiences: Grades 6-8, Grades 9-12

Primary Subjects: Algebra, Discrete, Geometry, Number and Operations

Related Topics: addition, arithmetic, arithmetic sequences, geometric sequences, graph, iteration, linear functions, multiplication, multiplier, negative number, pattern, positive number, pre-calculus, recursion, recursive functions, sequences

Students work step-by-step through the generation of a different Hilbert-like Curve (a fractal made from deforming a line by bending it), allowing them to explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: decimals, fractals, fractions, geometric sequences, geometry, iteration, length, pattern, self-similarity, sequences, surface area, symmetry

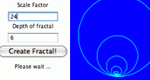
Generate complicated geometric fractals by specifying starting polygon and scale factor.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Geometry

Related Topics: fractals, geometry, logarithm, polygon, recursion, scale, self-similarity

Step through the generation of a Hilbert Curve -- a fractal made from deforming a line by bending it, and explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: chaos, fractals, geometric sequences, geometry, iteration, length, lines, pattern, recursion, self-similarity, sequences

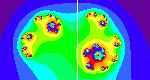
Enter a complex value for "c" in the form of an ordered pair of real numbers. The applet draws the fractal Julia set for that seed value.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: complex number, coordinate plane, coordinate system, fractals, iteration, julia set, mandelbrot set, recursion, recursive functions, sets

Step through the generation of the Koch Snowflake -- a fractal made from deforming the sides of a triangle, and explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: decimals, fractals, geometric sequences, infinity, iteration, lines, pre-calculus, recursion, self-similarity, sequences

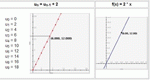
Graph recursive functions by defining f(0)=C and defining f(n) based on f(n-1).

Audiences: Grades 9-12, Undergraduate

Primary Subjects: Algebra, Discrete, Graphs, Number and Operations

Related Topics: algebra, arithmetic sequences, cartesian coordinate, coordinate plane, functions, geometric sequences, graph, iteration, recursion, recursive functions, sequences

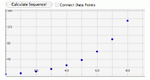
Learn about number patterns in sequences and recursions by specifying a starting number, multiplier, and add-on. The numbers in the sequence are displayed on a graph, and they are also listed below the graph.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Algebra, Discrete, Graphs, Number and Operations

Related Topics: addition, arithmetic, arithmetic sequences, cartesian coordinate, coordinate plane, decimals, geometric sequences, graph, iteration, multiplication, pre-calculus, recursion, recursive functions, sequences

Step through the generation of Sierpinski's Carpet -- a fractal made from subdividing a square into nine smaller squares and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: algebra, area, fractals, fractions, geometric sequences, iteration, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences

Step through the generation of Sierpinski's Triangle -- a fractal made from subdividing a triangle into four smaller triangles and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: dimension, fractals, fractions, geometric sequences, geometry, iteration, length, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences, symmetry, triangle

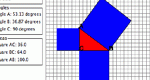
Learn about how the Pythagorean Theorem works through investigating the standard geometric proof. Parameters: Sizes of the legs of the triangle.

Audiences: Grades 6-8, Grades 9-12

Primary Subjects: Geometry, Trigonometry

Related Topics: algebra, angles, area, coordinate plane, distance, geometry, length, pythagorean theorem, slides, solving equations, squares, triangle, triangles, trigonometry

Explore fractals by investigating the relationships between the Mandelbrot set and Julia sets.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: chaos, complex number, coordinate, coordinate plane, exponents, fractals, functions, geometric sequences, geometry, iteration, julia set, mandelbrot set, pattern, recursion, recursive functions, self-similarity, sets

Enter two complex numbers (z and c) as ordered pairs of real numbers, then click a button to iterate step by step. The iterates are graphed in the x-y plane and printed out in table form. This is an introduction to the idea of prisoners/escapees in iterated functions and the calculation of fractal Julia sets.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Algebra, Geometry, Graphs, Number and Operations

Related Topics: complex number, coordinate plane, coordinate system, exponents, fractals, functions, graph, infinity, iteration, julia set, mandelbrot set, recursion, recursive functions, sets