Aligned Resources

Students consider the patterns that emerge from agent models and geometric fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Geometry, Modeling

Related Topics: agent modeling, fractals, pattern, recursion, self-similarity

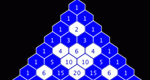
Uses modular (clock) arithmetic to find patterns in Pascal's Triangle.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: addition, arithmetic, division, divisors, integers, modular, pascal's triangle, pascals triangle, pattern, remainders, sum, triangle, whole numbers

Outlines the approach to building fractals by cutting out portions of plane figures.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: area, distance, fractals, fractions, generator, geometric sequences, geometry, infinity, initiator, iteration, length, limit, lines, multiplication, pattern, percents, perimeter, recursion, scale, segment, self-similarity, sequences, sets

Introduces students to arithmetic and geometric sequences. Students explore further through producing sequences by varying the starting number, multiplier, and add-on.

Audiences: Grades 6-8, Grades 9-12

Primary Subjects: Algebra, Discrete, Geometry, Number and Operations

Related Topics: addition, arithmetic, arithmetic sequences, geometric sequences, graph, iteration, linear functions, multiplication, multiplier, negative number, pattern, positive number, pre-calculus, recursion, recursive functions, sequences

Looks at how Pascal's Triangle can be used to generate Sierpinski triangle-like results.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: area, arithmetic, combinatorics, distance, division, factors, fractals, fractions, generator, geometric sequences, geometry, infinity, initiator, integers, iteration, length, limit, lines, multiples, multiplication, pascals triangle, pattern, percents, perimeter, quotient, recursion, remainders, scale, segment, self-similarity, sequences, sets, whole numbers

Introduces students to the idea of finding number patterns in the generation of several different types of fractals.

Audiences: Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: area, arithmetic, chaos, decimals, dimension, fractals, fractions, geometric sequences, geometry, graph, iteration, length, lines, pattern, pythagorean theorem, rectangles, recursion, segment, self-similarity, sequences, surface area, symmetry, triangle

Shows students that number patterns exist in the Pascal's Triangle, and reinforces student's ability to identify patterns.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: arithmetic, binomial, chaos, coefficient, combinatorics, decimals, dimension, division, divisors, factors, fractals, fractions, geometric sequences, geometry, infinity, integers, iteration, length, lines, multiples, multiplication, pascal's triangle, pattern, probability, rectangles, recursion, remainders, segment, self-similarity, sequences, surface area, symmetry, triangle, whole numbers

Students learn to identify a variety of patterns using sequences and tessellations.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: addition, arithmetic, arithmetic sequences, geometric sequences, hexagon, iteration, multiplication, pattern, planes, polygon, recursion, recursive functions, sequences, squares, symmetry, tessellations, triangle

In this lesson, students explore sets, elements, and Venn diagrams.

Audiences: Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: counting, element, integers, intersection, pattern, sets, union, venn diagram, whole numbers

Examines plane symmetry.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Geometry

Related Topics: angles, area, geometry, glides, hexagon, illusion, length, pattern, planes, polygon, rectangles, reflections, regular, rotation, segment, squares, symmetry, tessellations, transformation, translation, triangle

Help students learn about classifying numbers into various categories through answering questions about Venn Diagrams.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Number and Operations

Related Topics: element, pattern, sets, venn diagram

Students work step-by-step through the generation of a different Hilbert-like Curve (a fractal made from deforming a line by bending it), allowing them to explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: decimals, fractals, fractions, geometric sequences, geometry, iteration, length, pattern, self-similarity, sequences, surface area, symmetry

Learn about fractions between 0 and 1 by repeatedly deleting portions of a line segment, and also learn about properties of fractal objects. Parameter: fraction of the segment to be deleted each time.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: fractals, fractions, geometric sequences, pattern, pre-calculus, recursion, sequences, sets

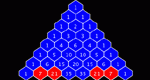
Color numbers in Pascal's Triangle by rolling a number and then clicking on all entries that are multiples of the number rolled, thereby practicing multiplication tables, investigating number patterns, and investigating fractal patterns. Coloring Multiples in Pascal's Triangle is one of the Interactivate assessment explorers.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: algebra, combinatorics, division, divisors, factors, fractals, integers, multiples, pascal's triangle, pascals triangle, pattern, triangle, whole numbers

Color numbers in Pascal's Triangle by rolling a number and then clicking on all entries that have the same remainder when divided by the number rolled, thereby practicing division and remainders, investigating number patterns, and investigating fractal patterns. Coloring Remainders in Pascal's Triangle is one of the Interactivate assessment explorers.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: algebra, combinatorics, division, divisors, factors, fractals, integers, modular, pascal's triangle, pascals triangle, pattern, remainders, triangle, whole numbers

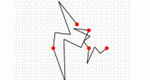
Create your own fractals by drawing a "line deformation rule" and stepping through the generation of a geometric fractal. Parameters: Grid type, number of bending points on the line.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Geometry, Number and Operations

Related Topics: chaos, fractals, geometric sequences, iteration, pattern, pre-calculus, recursion, scale, self-similarity, sequences, symmetry, transformation

Build a "floor tile" by dragging the corners of a quadrilateral. Learn about tessellation of quadrilateral figures when the shape you built is tiled over an area.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Geometry

Related Topics: angles, area, coordinate plane, coordinate system, length, pattern, planes, quadrilaterals, rectangles, reflections, rhombus, rotation, slides, symmetry, tessellations, transformation, translation

Step through the generation of a Hilbert Curve -- a fractal made from deforming a line by bending it, and explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: chaos, fractals, geometric sequences, geometry, iteration, length, lines, pattern, recursion, self-similarity, sequences

Step through the generation of the Koch Snowflake -- a fractal made from deforming the sides of a triangle, and explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: decimals, fractals, geometric sequences, infinity, iteration, lines, pre-calculus, recursion, self-similarity, sequences

Recognize patterns in a series of shapes, numbers, or letters. After determining the pattern, the student fills in the missing pieces. Three levels of difficulty are available.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Number and Operations

Related Topics: arithmetic, arithmetic sequences, iteration, pattern, sequences

Step through the generation of Sierpinski's Carpet -- a fractal made from subdividing a square into nine smaller squares and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: algebra, area, fractals, fractions, geometric sequences, iteration, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences

Step through the generation of Sierpinski's Triangle -- a fractal made from subdividing a triangle into four smaller triangles and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: dimension, fractals, fractions, geometric sequences, geometry, iteration, length, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences, symmetry, triangle

Classify various objects into categories in a Venn Diagram. Learn how categories in Venn Diagrams work. Venn Diagrams is one of the Interactivate assessment explorers.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Algebra, Discrete, Geometry, Graphs, Number and Operations

Related Topics: sets, venn diagram