Aligned Resources

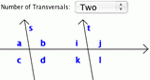
Introduces students to acute, obtuse, and right angles as well as relationships between angles formed by parallel lines crossed by a transversal.

Audiences: Grades 6-8, Grades 9-12

Primary Subjects: Geometry

Related Topics: acute, adjacent, alternate exterior, alternate interior, angles, corresponding, geometry, intersection, lines, obtuse, rays, right angle, transversal, vertical

Outlines the approach to playing the chaos game and how it relates to geometric fractals.

Audiences: Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Geometry, Number and Operations, Probability

Related Topics: chaos, experimental probability, fractals, fractions, geometric probability, infinity, iteration, outcomes, pattern, percents, probability, probability simulation, random number, recursion, self-similarity, theoretical probability, triangle

Explores lines, planes, angles, and polygons in tessellations.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Geometry

Related Topics: angles, area, flips, geometry, glides, hexagon, length, lines, pattern, perimeter, planes, polygon, rectangles, reflections, regular, rotation, slides, squares, symmetry, tessellations, triangle

Introduces students to the idea of finding number patterns in the generation of several different types of fractals.

Audiences: Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: area, arithmetic, chaos, decimals, dimension, fractals, fractions, geometric sequences, geometry, graph, iteration, length, lines, pattern, pythagorean theorem, rectangles, recursion, segment, self-similarity, sequences, surface area, symmetry, triangle

A capstone lesson to allow students to build a working definition of fractal.

Audiences: Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: area, chaos, dimension, distance, experimental probability, exponents, fractals, fractions, generator, geometric probability, geometric sequences, geometry, infinity, initiator, iteration, length, limit, lines, logarithm, multiplication, outcomes, pattern, percents, perimeter, probability, random number, recursion, scale, segment, self-similarity, sequences, sets, theoretical probability, triangle

Examines plane symmetry.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Geometry

Related Topics: angles, area, geometry, glides, hexagon, illusion, length, pattern, planes, polygon, rectangles, reflections, regular, rotation, segment, squares, symmetry, tessellations, transformation, translation, triangle

Introduces all of the 2 variable function and prisoner/escapee notions necessary to understand the Mandelbrot set.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: chaos, complex number, coordinate, coordinate plane, coordinate system, division, escape, exponents, fractals, functions, geometric sequences, geometry, infinity, iteration, julia set, mandelbrot set, multiplication, pattern, planes, prisoner, radius, recursion, recursive functions, self-similarity, sets, symmetry

Introduces students to concepts of transformations.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Algebra, Geometry

Related Topics: angles, cartesian coordinate, coordinate plane, coordinate system, dimension, distance, flips, geometry, glides, graph, hexagon, image, parallelogram, pattern, planes, polygon, pre-image, reflections, rotation, squares, symmetry, tessellations, transformation, translation, transpose, triangles

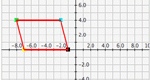
Build your own polygon and transform it in the Cartesian coordinate system. Experiment with reflections across any line, revolving around any line (which yields a 3-D image), rotations about any point, and translations in any direction.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Algebra, Calculus, Geometry, Graphs

Related Topics: angles, calculus, coordinate, coordinate plane, coordinate system, flips, geometry, glides, graph, polygon, polyhedra, reflections, rotation, symmetry, transformation, translation, transpose

Practice your knowledge of acute, obtuse, and alternate angles. Also, practice relationships between angles - vertical, adjacent, alternate, same-side, and corresponding. Angles is one of the Interactivate assessment explorers.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Geometry

Related Topics: acute, angles, assessment, geometry, lines, obtuse, parallel

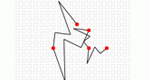
Students work step-by-step through the generation of a different Hilbert-like Curve (a fractal made from deforming a line by bending it), allowing them to explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: decimals, fractals, fractions, geometric sequences, geometry, iteration, length, pattern, self-similarity, sequences, surface area, symmetry

Create your own fractals by drawing a "line deformation rule" and stepping through the generation of a geometric fractal. Parameters: Grid type, number of bending points on the line.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Geometry, Number and Operations

Related Topics: chaos, fractals, geometric sequences, iteration, pattern, pre-calculus, recursion, scale, self-similarity, sequences, symmetry, transformation

Build a "floor tile" by dragging the corners of a quadrilateral. Learn about tessellation of quadrilateral figures when the shape you built is tiled over an area.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Geometry

Related Topics: angles, area, coordinate plane, coordinate system, length, pattern, planes, quadrilaterals, rectangles, reflections, rhombus, rotation, slides, symmetry, tessellations, transformation, translation

Step through the generation of a Hilbert Curve -- a fractal made from deforming a line by bending it, and explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: chaos, fractals, geometric sequences, geometry, iteration, length, lines, pattern, recursion, self-similarity, sequences

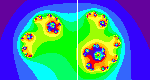
Enter a complex value for "c" in the form of an ordered pair of real numbers. The applet draws the fractal Julia set for that seed value.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: complex number, coordinate plane, coordinate system, fractals, iteration, julia set, mandelbrot set, recursion, recursive functions, sets

Step through the generation of the Koch Snowflake -- a fractal made from deforming the sides of a triangle, and explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: decimals, fractals, geometric sequences, infinity, iteration, lines, pre-calculus, recursion, self-similarity, sequences

Step through the generation of Sierpinski's Carpet -- a fractal made from subdividing a square into nine smaller squares and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: algebra, area, fractals, fractions, geometric sequences, iteration, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences

Step through the generation of Sierpinski's Triangle -- a fractal made from subdividing a triangle into four smaller triangles and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: dimension, fractals, fractions, geometric sequences, geometry, iteration, length, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences, symmetry, triangle

Explore fractals by investigating the relationships between the Mandelbrot set and Julia sets.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: chaos, complex number, coordinate, coordinate plane, exponents, fractals, functions, geometric sequences, geometry, iteration, julia set, mandelbrot set, pattern, recursion, recursive functions, self-similarity, sets

Explore the world of translations, reflections, and rotations in the Cartesian coordinate system by transforming squares, triangles and parallelograms. Parameters: Shape, x or y translation, x or y reflection, angle of rotation.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Geometry, Graphs

Related Topics: cartesian coordinate, coordinate plane, coordinate system, flips, geometry, glides, graph, hexagon, image, polygon, pre-image, reflections, rotation, symmetry, transformation, translation, transpose, triangle

Build your own polygon and transform it in the Cartesian coordinate system. Experiment with reflections across any line, rotations about any point, and translations in any direction. Parameters: Shape, x or y translation, x or y reflection, angle of rotation

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Geometry, Graphs

Related Topics: angles, cartesian coordinate, coordinate, coordinate plane, coordinate system, flips, geometry, glides, graph, image, linear equations, polygon, pre-image, reflections, rotation, symmetry, transformation, translation, transpose