Alaska Performance Standards
Grade 10
Geometry
The student demonstrates a conceptual understanding of geometric drawings or constructions.
Lessons (14)
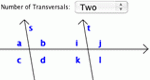
Introduces students to acute, obtuse, and right angles as well as relationships between angles formed by parallel lines crossed by a transversal.
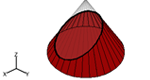
This lesson utilizes the concepts of cross-sections of three-dimensional figures to demonstrate the derivation of two-dimensional shapes.
Outlines the approach to playing the chaos game and how it relates to geometric fractals.
Outlines the approach to building fractals by cutting out portions of plane figures.
Explores lines, planes, angles, and polygons in tessellations.
Introduces students to the ideas involved in understanding fractals.
Looks at how irregular fractals can be generated and how they fit into computer graphics.
Introduces students to the idea of finding number patterns in the generation of several different types of fractals.
Students learn about how probability can be represented using geometry.
A capstone lesson to allow students to build a working definition of fractal.
Examines plane symmetry.
Introduces all of the 2 variable function and prisoner/escapee notions necessary to understand the Mandelbrot set.
Introduces students to concepts of transformations.
Explore the mathematical nature of art and tilings and looks at the role of math in nature and our culture.
Activities (20)
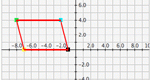
Build your own polygon and transform it in the Cartesian coordinate system. Experiment with reflections across any line, revolving around any line (which yields a 3-D image), rotations about any point, and translations in any direction.
Practice your knowledge of acute, obtuse, and alternate angles. Also, practice relationships between angles - vertical, adjacent, alternate, same-side, and corresponding. Angles is one of the Interactivate assessment explorers.
Students work step-by-step through the generation of a different Hilbert-like Curve (a fractal made from deforming a line by bending it), allowing them to explore number patterns in sequences and geometric properties of fractals.
Explore cross sections of different geometric solids: cone, double cone, cylinder, pyramid, and prism. Manipulate the cross section with slider bars, and see how the graphical representation changes.
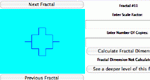
Create your own fractals by drawing a "line deformation rule" and stepping through the generation of a geometric fractal. Parameters: Grid type, number of bending points on the line.
Build a "floor tile" by dragging the corners of a quadrilateral. Learn about tessellation of quadrilateral figures when the shape you built is tiled over an area.
Determine the fractal dimensions of several line-deformation fractals. Input the scale factor and number of similar copies, and the dimension will be calculated. Fractal Dimensions is one of the Interactivate assessment explorers.
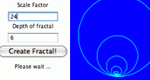
Generate complicated geometric fractals by specifying starting polygon and scale factor.
Step through the generation of a Hilbert Curve -- a fractal made from deforming a line by bending it, and explore number patterns in sequences and geometric properties of fractals.
Measure angles, distances, and areas in several different images (choices include maps, aerial photos, and others). A scale feature allows the user to set the scale used for measuring distances and areas.
Enter a complex value for "c" in the form of an ordered pair of real numbers. The applet draws the fractal Julia set for that seed value.
Step through the generation of the Koch Snowflake -- a fractal made from deforming the sides of a triangle, and explore number patterns in sequences and geometric properties of fractals.
Step through the generation of Sierpinski's Carpet -- a fractal made from subdividing a square into nine smaller squares and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.
Step through the generation of Sierpinski's Triangle -- a fractal made from subdividing a triangle into four smaller triangles and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.
Manipulate dimensions of polyhedra, and watch how the surface area and volume change. Parameters: Type of polyhedron, length, width and height. Surface Area and Volume one of the Interactivate assessment explorers.
Create a tessellation by deforming a triangle, rectangle or hexagon to form a polygon that tiles the plane. Corners of the polygons may be dragged, and corresponding edges of the polygons may be dragged. Parameters: Colors, starting polygon.
Play the Chaos Game by experimenting with probabilities. Learn about an apparently random process with a not-so-random, geometric fractal result.
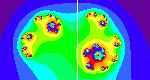
Explore fractals by investigating the relationships between the Mandelbrot set and Julia sets.
Explore the world of translations, reflections, and rotations in the Cartesian coordinate system by transforming squares, triangles and parallelograms. Parameters: Shape, x or y translation, x or y reflection, angle of rotation.
Build your own polygon and transform it in the Cartesian coordinate system. Experiment with reflections across any line, rotations about any point, and translations in any direction. Parameters: Shape, x or y translation, x or y reflection, angle of rotation