Aligned Resources

Introduces students to acute, obtuse, and right angles as well as relationships between angles formed by parallel lines crossed by a transversal.

Audiences: Grades 6-8, Grades 9-12

Primary Subjects: Geometry

Related Topics: acute, adjacent, alternate exterior, alternate interior, angles, corresponding, geometry, intersection, lines, obtuse, rays, right angle, transversal, vertical

Introduces students to arithmetic and geometric sequences. Students explore further through producing sequences by varying the starting number, multiplier, and add-on.

Audiences: Grades 6-8, Grades 9-12

Primary Subjects: Algebra, Discrete, Geometry, Number and Operations

Related Topics: addition, arithmetic, arithmetic sequences, geometric sequences, graph, iteration, linear functions, multiplication, multiplier, negative number, pattern, positive number, pre-calculus, recursion, recursive functions, sequences

Introduces students to length, perimeter and area.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Geometry

Related Topics: acute, addition, area, arithmetic, cartesian coordinate, coordinate plane, dimension, distance, geometry, length, multiplication, obtuse, perimeter, planes, polygon, pythagorean theorem, rectangles, subtraction, triangle, width

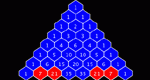
Looks at how Pascal's Triangle can be used to generate Sierpinski triangle-like results.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: area, arithmetic, combinatorics, distance, division, factors, fractals, fractions, generator, geometric sequences, geometry, infinity, initiator, integers, iteration, length, limit, lines, multiples, multiplication, pascals triangle, pattern, percents, perimeter, quotient, recursion, remainders, scale, segment, self-similarity, sequences, sets, whole numbers

Students learn to identify a variety of patterns using sequences and tessellations.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: addition, arithmetic, arithmetic sequences, geometric sequences, hexagon, iteration, multiplication, pattern, planes, polygon, recursion, recursive functions, sequences, squares, symmetry, tessellations, triangle

Color numbers in Pascal's Triangle by rolling a number and then clicking on all entries that have the same remainder when divided by the number rolled, thereby practicing division and remainders, investigating number patterns, and investigating fractal patterns. Coloring Remainders in Pascal's Triangle is one of the Interactivate assessment explorers.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: algebra, combinatorics, division, divisors, factors, fractals, integers, modular, pascal's triangle, pascals triangle, pattern, remainders, triangle, whole numbers

Recognize patterns in a series of shapes, numbers, or letters. After determining the pattern, the student fills in the missing pieces. Three levels of difficulty are available.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Number and Operations

Related Topics: arithmetic, arithmetic sequences, iteration, pattern, sequences

Step through the generation of Sierpinski's Carpet -- a fractal made from subdividing a square into nine smaller squares and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: algebra, area, fractals, fractions, geometric sequences, iteration, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences

Step through the generation of Sierpinski's Triangle -- a fractal made from subdividing a triangle into four smaller triangles and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: dimension, fractals, fractions, geometric sequences, geometry, iteration, length, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences, symmetry, triangle