Aligned Resources

Introduces students to arithmetic and geometric sequences. Students explore further through producing sequences by varying the starting number, multiplier, and add-on.

Audiences: Grades 6-8, Grades 9-12

Primary Subjects: Algebra, Discrete, Geometry, Number and Operations

Related Topics: addition, arithmetic, arithmetic sequences, geometric sequences, graph, iteration, linear functions, multiplication, multiplier, negative number, pattern, positive number, pre-calculus, recursion, recursive functions, sequences

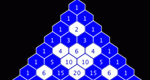
Shows students that number patterns exist in the Pascal's Triangle, and reinforces student's ability to identify patterns.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: arithmetic, binomial, chaos, coefficient, combinatorics, decimals, dimension, division, divisors, factors, fractals, fractions, geometric sequences, geometry, infinity, integers, iteration, length, lines, multiples, multiplication, pascal's triangle, pattern, probability, rectangles, recursion, remainders, segment, self-similarity, sequences, surface area, symmetry, triangle, whole numbers

Students learn to identify a variety of patterns using sequences and tessellations.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: addition, arithmetic, arithmetic sequences, geometric sequences, hexagon, iteration, multiplication, pattern, planes, polygon, recursion, recursive functions, sequences, squares, symmetry, tessellations, triangle

Learn about fractions between 0 and 1 by repeatedly deleting portions of a line segment, and also learn about properties of fractal objects. Parameter: fraction of the segment to be deleted each time.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: fractals, fractions, geometric sequences, pattern, pre-calculus, recursion, sequences, sets

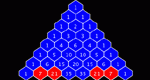
Color numbers in Pascal's Triangle by rolling a number and then clicking on all entries that are multiples of the number rolled, thereby practicing multiplication tables, investigating number patterns, and investigating fractal patterns. Coloring Multiples in Pascal's Triangle is one of the Interactivate assessment explorers.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: algebra, combinatorics, division, divisors, factors, fractals, integers, multiples, pascal's triangle, pascals triangle, pattern, triangle, whole numbers

Color numbers in Pascal's Triangle by rolling a number and then clicking on all entries that have the same remainder when divided by the number rolled, thereby practicing division and remainders, investigating number patterns, and investigating fractal patterns. Coloring Remainders in Pascal's Triangle is one of the Interactivate assessment explorers.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: algebra, combinatorics, division, divisors, factors, fractals, integers, modular, pascal's triangle, pascals triangle, pattern, remainders, triangle, whole numbers

Recognize patterns in a series of shapes, numbers, or letters. After determining the pattern, the student fills in the missing pieces. Three levels of difficulty are available.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Number and Operations

Related Topics: arithmetic, arithmetic sequences, iteration, pattern, sequences

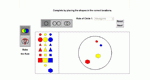
Sort colored shapes into a Venn diagram based on various characteristics. Venn Diagram Shape Sorter is one of the Interactivate assessment explorers.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Discrete, Geometry, Graphs, Number and Operations

Related Topics: pattern, sets, sorter, venn diagram

Step through the generation of Sierpinski's Carpet -- a fractal made from subdividing a square into nine smaller squares and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: algebra, area, fractals, fractions, geometric sequences, iteration, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences

Step through the generation of Sierpinski's Triangle -- a fractal made from subdividing a triangle into four smaller triangles and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: dimension, fractals, fractions, geometric sequences, geometry, iteration, length, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences, symmetry, triangle

Step through the tortoise and hare race, based on Zeno's paradox, to learn about the multiplication of fractions and about convergence of an infinite sequence of numbers.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Discrete, Number and Operations

Related Topics: decimals, distance, fractals, geometric sequences, infinity, iteration, length, logarithm, multiplication, pattern, percentages, percents, proportion, rational numbers, recursion, recursive functions, self-similarity, sequences

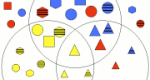
Sort colored shapes into a three circle Venn Diagram.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Discrete, Geometry, Number and Operations, Science

Related Topics: pattern, sets, venn diagram