Aligned Resources

Lesson plan to help students understand independent and dependent variables through a fire probability simulation.

Audiences: Grades 6-8, Grades 9-12

Primary Subjects: Algebra, Modeling

Related Topics: algebra, dependent, independent, input, output, probability, variable

Students practice arithmetic skills. Can be tailored for practice of all types of single operation arithmetic ranging from simple addition to operations with integers and decimals.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Number and Operations

Related Topics: addition, algorithm, arithmetic, coordinate, data, decimals, division, fractions, graph, integers, linear equations, linear functions, multiplication, subtraction

In this lesson, students explore sets, elements, and Venn diagrams.

Audiences: Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: counting, element, integers, intersection, pattern, sets, union, venn diagram, whole numbers

Students run a simulation of how a fire will spread through a stand of trees, learning about probability and chaos. Parameters: Forest density, wind direction, size of forest.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Fractions, Modeling, Probability

Related Topics: agent modeling, chaos, conditional probability, experimental probability, iteration, percentages, percents, probability simulation, proportion, simulation, skewed distribution, variance

Run a simulation of how a fire spreads through a stand of trees, learning about probability and chaos. Track the results of multiple burns and use the data to draw conclusions.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Modeling, Probability, Statistics

Related Topics: agent modeling, chaos, conditional probability, experimental probability, probability simulation, simulation, theoretical probability

Run a simulation of how a fire will spread through a stand of trees, learning about probability and chaos. Parameters: Probability that a tree will set fire to each of its eight neighbors.

Audiences: Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Modeling, Probability

Related Topics: agent modeling, chaos, events, experimental probability, geometric probability, percentages, percents, probability simulation, proportion, recursion, simulation, statistics, theoretical probability, variance

Run a simulation of how a fire will spread through a stand of trees, learning about probability and chaos. Parameters: Probability that a tree catches fire if its neighbor is on fire.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Modeling, Probability

Related Topics: agent modeling, chaos, decimals, events, experimental probability, outcomes, percentages, percents, proportion, simulation, squares, theoretical probability, variance

Students can create graphs of functions entered as algebraic expressions -- similar to a graphing calculator.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Algebra, Calculus, Graphs, Trigonometry

Related Topics: algebra, calculus, cartesian coordinate, coordinate plane, cosecant, cosine, cotangent, functions, graph, inverse, linear equations, linear functions, logarithm, parabola, polynomial, positive part of the operand, pre-calculus, range, secant, sine, slope, tangent, trigonometry

Create graphs of functions and sets of ordered pairs on the same coordinate plane. This is like a graphing calculator with advanced viewing options.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Algebra, Calculus, Graphs, Statistics, Trigonometry

Related Topics: algebra, calculus, cartesian coordinate, coordinate, coordinate plane, coordinate system, cosecant, cosine, cotangent, curve fitting, data plot, exponential, exponents, function properties, functions, graph, graph theory, intervals, linear equations, linear functions, logarithm, parabola, polynomial, positive part of the operand, pre-calculus, range, secant, sine, slope, tangent, trigonometry

Step through the generation of the Koch Snowflake -- a fractal made from deforming the sides of a triangle, and explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: decimals, fractals, geometric sequences, infinity, iteration, lines, pre-calculus, recursion, self-similarity, sequences

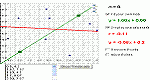
Plot a bivariate data set, determine the line of best fit for their data, and then check the accuracy of your line of best fit.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Algebra, Calculus, Graphs, Statistics

Related Topics: calculus, cartesian coordinate, coordinate plane, correlation, curve fitting, data plot, deviations, residual, statistics

Step through the generation of Sierpinski's Carpet -- a fractal made from subdividing a square into nine smaller squares and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: algebra, area, fractals, fractions, geometric sequences, iteration, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences

Step through the generation of Sierpinski's Triangle -- a fractal made from subdividing a triangle into four smaller triangles and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: dimension, fractals, fractions, geometric sequences, geometry, iteration, length, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences, symmetry, triangle

Plot ordered pairs of numbers, either as a scatter plot or with the dots connected. Points are connected from right to left, rather than being connected in the order they are entered.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Algebra, Geometry, Graphs, Statistics

Related Topics: cartesian coordinate, coordinate plane, coordinate system, data plot, decimals, graph

Step through the tortoise and hare race, based on Zeno's paradox, to learn about the multiplication of fractions and about convergence of an infinite sequence of numbers.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Discrete, Number and Operations

Related Topics: decimals, distance, fractals, geometric sequences, infinity, iteration, length, logarithm, multiplication, pattern, percentages, percents, proportion, rational numbers, recursion, recursive functions, self-similarity, sequences