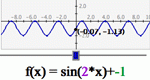NCTM
Grades 9-12
Algebra
Understand patterns, relations, and functions
Lessons (13)
Explores derivatives and the idea of infinity using a geometric interpretation of slope.
Demonstrates the connections between formulas and graphs.
Teaches distinguishing between possible and impossible graphs of functions as well as causes of graphical impossibility.
Introduces students to the ideas involved in understanding fractals.
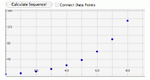
Introduces students to arithmetic and geometric sequences. Students explore further through producing sequences by varying the starting number, multiplier, and add-on.
Introduces the basic ideas needed for understanding linear functions.
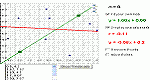
Students are introduced to correlation between two variables and the line of best fit.
Introduces students to the idea of finding number patterns in the generation of several different types of fractals.
Shows students that number patterns exist in the Pascal's Triangle, and reinforces student's ability to identify patterns.
Demonstrates the connections between formulas, graphs and words.
In this lesson, students explore sets, elements, and Venn diagrams.
Introduction to various algorithms for solving single-variable, linear equations.
Introduces all of the 2 variable function and prisoner/escapee notions necessary to understand the Mandelbrot set.
Activities (23)
Students work step-by-step through the generation of a different Hilbert-like Curve (a fractal made from deforming a line by bending it), allowing them to explore number patterns in sequences and geometric properties of fractals.
Decode encrypted messages to determine the form for an affine cipher, and practice your reasoning and arithmetic skills. Input your guesses for the multiplier and constant. Caesar Cipher III is one of the Interactivate assessment explorers.
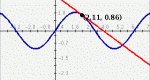
Enter a set of data points, then derive a function to fit those points. Manipulate the function on a coordinate plane using slider bars. Learn how each constant and coefficient affects the resulting graph.
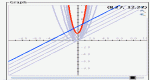
View the graph and the equation of the line tangent to any function at any point on the function.
This activity helps you understand how to balance an equation. You input the term and the operation. The activity uses that term and operates on both sides of the equation. It then displays the resulting equation. Equation Solver is one of the Interactivate assessment explorers.
A more advanced version of Slope Slider, this activity allows the manipulation of the constants and coefficients in any function thereby encouraging the user to explore the effects on the graph of the function by changing those numbers.
Students can create graphs of functions entered as algebraic expressions -- similar to a graphing calculator.
Create graphs of functions and sets of ordered pairs on the same coordinate plane. This is like a graphing calculator with advanced viewing options.
Step through the generation of a Hilbert Curve -- a fractal made from deforming a line by bending it, and explore number patterns in sequences and geometric properties of fractals.
This applet allows the user to make observations about the relationship between speed and position and how both of these are affected by initial velocity and the incline on which the biker is traveling.
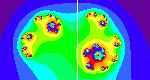
Enter a complex value for "c" in the form of an ordered pair of real numbers. The applet draws the fractal Julia set for that seed value.
Step through the generation of the Koch Snowflake -- a fractal made from deforming the sides of a triangle, and explore number patterns in sequences and geometric properties of fractals.
Enter a set of data points and a function or multiple functions, then manipulate those functions to fit those points. Manipulate the function on a coordinate plane using slider bars. Learn how each constant and coefficient affects the resulting graph.
Graph recursive functions by defining f(0)=C and defining f(n) based on f(n-1).
Plot a bivariate data set, determine the line of best fit for their data, and then check the accuracy of your line of best fit.
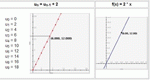
Learn about number patterns in sequences and recursions by specifying a starting number, multiplier, and add-on. The numbers in the sequence are displayed on a graph, and they are also listed below the graph.
Step through the generation of Sierpinski's Carpet -- a fractal made from subdividing a square into nine smaller squares and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.
Step through the generation of Sierpinski's Triangle -- a fractal made from subdividing a triangle into four smaller triangles and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.
Similar to other "flyers", Slope Slider uses slider bars to explore the effect of the multiplier and constant on a linear function of the form f(x)=mx+b. Explore the relationship between slope and intercept in the Cartesian coordinate system.
Explore fractals by investigating the relationships between the Mandelbrot set and Julia sets.
Enter two complex numbers (z and c) as ordered pairs of real numbers, then click a button to iterate step by step. The iterates are graphed in the x-y plane and printed out in table form. This is an introduction to the idea of prisoners/escapees in iterated functions and the calculation of fractal Julia sets.
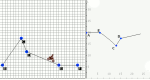
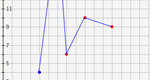
Learn about the vertical line test for functions by trying to connect points in the plane to build a function. When you have connected all of the points, you will be told if your graph is a valid graph of a function. Vertical Line Test is one of the Interactivate assessment explorers.
Students create linear inequalities and systems of linear inequalities on a coordinate plane. This is like a graphing calculator with advanced viewing options.