Aligned Resources

Comparing shapes with the same areas but different perimeters.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Geometry

Related Topics: area, comparing, geometry, integers, length, perimeter, polygon, rectangles, right angle, squares, width

Students learn about definite integrals through limits and Riemann sums

Audiences: Grades 9-12, Undergraduate

Primary Subjects: Algebra, Calculus

Related Topics: area, calculus, estimation, function properties, functions, graph, infinity, integral, integrate, intervals

Introduces students to the concept of perimeter.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Geometry

Related Topics: addition, algorithm, arithmetic, geometry, length, perimeter, planes, polygon, rectangles, squares, width

Introduces students to the concepts of surface area and volume.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Geometry

Related Topics: area, arithmetic, dimension, geometry, integers, length, polyhedra, prisms, surface area, volume

Students work step-by-step through the generation of a different Hilbert-like Curve (a fractal made from deforming a line by bending it), allowing them to explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: decimals, fractals, fractions, geometric sequences, geometry, iteration, length, pattern, self-similarity, sequences, surface area, symmetry

Learn the relationship between perimeter and area. A shape will be automatically generated with the perimeter that you choose. Calculate the area of this shape. Area Explorer is one of the Interactivate assessment explorers.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Geometry

Related Topics: addition, area, arithmetic, assessment, comparing, coordinate plane, geometry, length, perimeter, polygon, rectangles, squares

Learn about fractions between 0 and 1 by repeatedly deleting portions of a line segment, and also learn about properties of fractal objects. Parameter: fraction of the segment to be deleted each time.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: fractals, fractions, geometric sequences, pattern, pre-calculus, recursion, sequences, sets

Step through the generation of a Hilbert Curve -- a fractal made from deforming a line by bending it, and explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: chaos, fractals, geometric sequences, geometry, iteration, length, lines, pattern, recursion, self-similarity, sequences

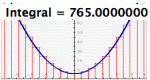
InteGreat! allows the user to visually explore the idea of integration through approximating the integral value with partitions. The user controls the number of partitions, the upper and lower limits, and the method used to estimate the integral.

Audiences: Grades 9-12, Undergraduate

Primary Subjects: Algebra, Calculus, Graphs

Related Topics: area, calculus, estimation, function properties, functions, graph, infinity, integral, integrate, intervals, limit

Enter a complex value for "c" in the form of an ordered pair of real numbers. The applet draws the fractal Julia set for that seed value.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: complex number, coordinate plane, coordinate system, fractals, iteration, julia set, mandelbrot set, recursion, recursive functions, sets

Step through the generation of the Koch Snowflake -- a fractal made from deforming the sides of a triangle, and explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: decimals, fractals, geometric sequences, infinity, iteration, lines, pre-calculus, recursion, self-similarity, sequences

Learn the relationship between perimeter and area. A shape will be automatically generated with the area that you choose. Calculate the perimeter of this shape. Perimeter Explorer is one of the Interactivate assessment explorers.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Geometry

Related Topics: area, arithmetic, assessment, comparing, coordinate plane, coordinate system, geometry, length, perimeter, polygon, rectangles, squares

This activity operates in one of two modes: auto draw and create shape mode, allowing you to explore relationships between area and perimeter. Shape Builder is one of the Interactivate assessment explorers.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Geometry

Related Topics: area, assessment, comparing, geometry, perimeter

Learn the relationship between perimeter and area. A random shape will be automatically generated. Calculate the area and perimeter of this shape. Shape Explorer is one of the Interactivate assessment explorers.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Geometry

Related Topics: area, arithmetic, assessment, comparing, geometry, length, perimeter, polygon, rectangles, squares

Step through the generation of Sierpinski's Carpet -- a fractal made from subdividing a square into nine smaller squares and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: algebra, area, fractals, fractions, geometric sequences, iteration, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences

Step through the generation of Sierpinski's Triangle -- a fractal made from subdividing a triangle into four smaller triangles and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: dimension, fractals, fractions, geometric sequences, geometry, iteration, length, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences, symmetry, triangle

Manipulate dimensions of polyhedra, and watch how the surface area and volume change. Parameters: Type of polyhedron, length, width and height. Surface Area and Volume one of the Interactivate assessment explorers.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Geometry

Related Topics: assessment, dimension, geometry, length, polyhedra, prisms, surface area, volume

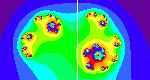
Explore fractals by investigating the relationships between the Mandelbrot set and Julia sets.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: chaos, complex number, coordinate, coordinate plane, exponents, fractals, functions, geometric sequences, geometry, iteration, julia set, mandelbrot set, pattern, recursion, recursive functions, self-similarity, sets

Step through the tortoise and hare race, based on Zeno's paradox, to learn about the multiplication of fractions and about convergence of an infinite sequence of numbers.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Discrete, Number and Operations

Related Topics: decimals, distance, fractals, geometric sequences, infinity, iteration, length, logarithm, multiplication, pattern, percentages, percents, proportion, rational numbers, recursion, recursive functions, self-similarity, sequences

Calculate the area of a triangle drawn on a grid. Learn about areas of triangles and about the Cartesian coordinate system. Triangle Explorer is one of the Interactivate assessment explorers.

Audiences: Grades 6-8, Grades 9-12

Primary Subjects: Geometry

Related Topics: acute, area, assessment, cartesian coordinate, coordinate plane, distance, geometry, length, pythagorean theorem, triangle, triangles

Enter two complex numbers (z and c) as ordered pairs of real numbers, then click a button to iterate step by step. The iterates are graphed in the x-y plane and printed out in table form. This is an introduction to the idea of prisoners/escapees in iterated functions and the calculation of fractal Julia sets.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Algebra, Geometry, Graphs, Number and Operations

Related Topics: complex number, coordinate plane, coordinate system, exponents, fractals, functions, graph, infinity, iteration, julia set, mandelbrot set, recursion, recursive functions, sets