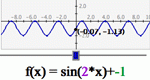Patterns

Shows students that number patterns exist in the Pascal's Triangle, and reinforces student's ability to identify patterns.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: arithmetic, binomial, chaos, coefficient, combinatorics, decimals, dimension, division, divisors, factors, fractals, fractions, geometric sequences, geometry, infinity, integers, iteration, length, lines, multiples, multiplication, pascal's triangle, pattern, probability, rectangles, recursion, remainders, segment, self-similarity, sequences, surface area, symmetry, triangle, whole numbers

Students learn to identify a variety of patterns using sequences and tessellations.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: addition, arithmetic, arithmetic sequences, geometric sequences, hexagon, iteration, multiplication, pattern, planes, polygon, recursion, recursive functions, sequences, squares, symmetry, tessellations, triangle

Students work step-by-step through the generation of a different Hilbert-like Curve (a fractal made from deforming a line by bending it), allowing them to explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: decimals, fractals, fractions, geometric sequences, geometry, iteration, length, pattern, self-similarity, sequences, surface area, symmetry

Enter a set of data points, then derive a function to fit those points. Manipulate the function on a coordinate plane using slider bars. Learn how each constant and coefficient affects the resulting graph.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Algebra, Graphs, Modeling, Statistics, Trigonometry

Related Topics: algebra, cartesian coordinate, coordinate, coordinate plane, coordinate system, cosecant, cosine, cotangent, curve fitting, data plot, deviations, exponential, exponents, function properties, functions, graph, grouping, integers, intervals, inverse, linear equations, linear functions, logarithm, multiplication, parabola, polynomial, positive part of the operand, pre-calculus, range, secant, sine, slope, tangent, trigonometry

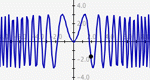
A more advanced version of Slope Slider, this activity allows the manipulation of the constants and coefficients in any function thereby encouraging the user to explore the effects on the graph of the function by changing those numbers.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Algebra, Calculus, Graphs, Trigonometry

Related Topics: algebra, bell curve, calculus, cartesian coordinate, coordinate plane, coordinate system, cosine, decimals, exponential, flyer, function properties, functions, graph, intervals, inverse, linear equations, linear functions, lines, logarithm, parabola, polynomial, pre-calculus, range, sine, slope, tangent, translation, trigonometry

Students investigate very simple functions by trying to guess the algebraic form from inputs and outputs. Function Machine is one of the Interactivate assessment explorers.

Audiences: Grades 6-8, Grades 9-12

Primary Subjects: Algebra, Discrete

Related Topics: addition, algebra, arithmetic, assessment, function machine, functions, input, integers, linear equations, multiplication, output, subtraction

Create graphs of functions and sets of ordered pairs on the same coordinate plane. This is like a graphing calculator with advanced viewing options.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Algebra, Calculus, Graphs, Statistics, Trigonometry

Related Topics: algebra, calculus, cartesian coordinate, coordinate, coordinate plane, coordinate system, cosecant, cosine, cotangent, curve fitting, data plot, exponential, exponents, function properties, functions, graph, graph theory, intervals, linear equations, linear functions, logarithm, parabola, polynomial, positive part of the operand, pre-calculus, range, secant, sine, slope, tangent, trigonometry

Step through the generation of a Hilbert Curve -- a fractal made from deforming a line by bending it, and explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: chaos, fractals, geometric sequences, geometry, iteration, length, lines, pattern, recursion, self-similarity, sequences

Step through the generation of the Koch Snowflake -- a fractal made from deforming the sides of a triangle, and explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: decimals, fractals, geometric sequences, infinity, iteration, lines, pre-calculus, recursion, self-similarity, sequences

Review the properties of functions by looking at ten different curves and deciding whether or not they meet the criteria for a graph of a function. This activity simply displays the curves - it does not quiz the user.

Audiences: Grades 6-8, Grades 9-12

Primary Subjects: Algebra, Discrete

Related Topics: coordinate plane, function properties, functions, graph, linear functions, lines, pre-calculus, vertical line test

Step through the generation of Sierpinski's Carpet -- a fractal made from subdividing a square into nine smaller squares and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: algebra, area, fractals, fractions, geometric sequences, iteration, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences

Step through the generation of Sierpinski's Triangle -- a fractal made from subdividing a triangle into four smaller triangles and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: dimension, fractals, fractions, geometric sequences, geometry, iteration, length, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences, symmetry, triangle

Plot ordered pairs of numbers, either as a scatter plot or with the dots connected. Points are connected from right to left, rather than being connected in the order they are entered.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Algebra, Geometry, Graphs, Statistics

Related Topics: cartesian coordinate, coordinate plane, coordinate system, data plot, decimals, graph

Enter two complex numbers (z and c) as ordered pairs of real numbers, then click a button to iterate step by step. The iterates are graphed in the x-y plane and printed out in table form. This is an introduction to the idea of prisoners/escapees in iterated functions and the calculation of fractal Julia sets.

Audiences: Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Algebra, Geometry, Graphs, Number and Operations

Related Topics: complex number, coordinate plane, coordinate system, exponents, fractals, functions, graph, infinity, iteration, julia set, mandelbrot set, recursion, recursive functions, sets