Fractions

Students work step-by-step through the generation of a different Hilbert-like Curve (a fractal made from deforming a line by bending it), allowing them to explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: decimals, fractals, fractions, geometric sequences, geometry, iteration, length, pattern, self-similarity, sequences, surface area, symmetry

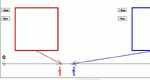
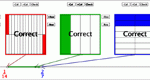
The same as "Bounded Fraction Pointer" but there is no arrow to help the user determine the value of a fraction between the two endpoints. Bounded Fraction Finder is one of the Interactivate assessment explorers.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Fractions, Number and Operations

Related Topics: comparing, fractions, number line, ordering, rational numbers

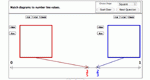
Determine the value of two fractions you have chosen (which are represented as points on a number line). Then find a fraction whose value is between your two fractions (using an arrow on the number line as a guide) and determine its value. Bounded Fraction Pointer is one of the Interactivate assessment explorers.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Fractions, Number and Operations

Related Topics: comparing, fractions, number line, ordering, rational numbers

Learn about fractions between 0 and 1 by repeatedly deleting portions of a line segment, and also learn about properties of fractal objects. Parameter: fraction of the segment to be deleted each time.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Geometry, Number and Operations

Related Topics: fractals, fractions, geometric sequences, pattern, pre-calculus, recursion, sequences, sets

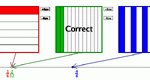
Visually represent two unique fractions that are equivalent to a given fraction. The fractional value is shown on a number line after you check to see if your fraction is correct. Equivalent Fraction Finder is one of the Interactivate assessment explorers.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Fractions, Number and Operations

Related Topics: comparing, fractions, identity, multiples, number line, proportion, rational numbers

Visually represent two unique fractions that are equivalent to a given fraction. The fractional value is shown on a number line as you color in the fraction. Equivalent Fraction Pointer is one of the Interactivate assessment explorers.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Fractions, Number and Operations

Related Topics: comparing, fractions, identity, multiples, number line, ordering, proportion, rational numbers

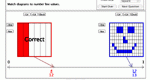
Determine the value of two given fractions represented as points on a number line. Then find a fraction whose value is between the two given fractions and determine its value. Fraction Finder is one of the Interactivate assessment explorers.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Fractions, Number and Operations

Related Topics: arithmetic, comparing, fractions, number line, ordering, rational numbers, subtraction

Determine the value of two given fractions represented as points on a number line. Then find a fraction whose value is between the two given fractions (using an arrow on the number line as a guide) and determine its value. Fraction Pointer is one of the Interactivate assessment explorers.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Fractions, Number and Operations

Related Topics: arithmetic, comparing, fractions, number line, ordering, rational numbers, subtraction

Step through the generation of a Hilbert Curve -- a fractal made from deforming a line by bending it, and explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: chaos, fractals, geometric sequences, geometry, iteration, length, lines, pattern, recursion, self-similarity, sequences

Step through the generation of the Koch Snowflake -- a fractal made from deforming the sides of a triangle, and explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12, Undergraduate

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: decimals, fractals, geometric sequences, infinity, iteration, lines, pre-calculus, recursion, self-similarity, sequences

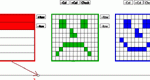
Step through the generation of Sierpinski's Carpet -- a fractal made from subdividing a square into nine smaller squares and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: algebra, area, fractals, fractions, geometric sequences, iteration, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences

Step through the generation of Sierpinski's Triangle -- a fractal made from subdividing a triangle into four smaller triangles and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.

Audiences: Grades 3-5, Grades 6-8, Grades 9-12

Primary Subjects: Discrete, Fractions, Geometry, Number and Operations

Related Topics: dimension, fractals, fractions, geometric sequences, geometry, iteration, length, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences, symmetry, triangle

Step through the tortoise and hare race, based on Zeno's paradox, to learn about the multiplication of fractions and about convergence of an infinite sequence of numbers.

Audiences: Grades 3-5, Grades 6-8

Primary Subjects: Discrete, Number and Operations

Related Topics: decimals, distance, fractals, geometric sequences, infinity, iteration, length, logarithm, multiplication, pattern, percentages, percents, proportion, rational numbers, recursion, recursive functions, self-similarity, sequences