Students work step-by-step through the generation of a different Hilbert-like Curve (a fractal made from deforming a line by bending it), allowing them to explore number patterns in sequences and geometric properties of fractals.
Audiences:
Grades 3-5, Grades 6-8, Grades 9-12
Primary Subjects:
Discrete, Fractions, Geometry, Number and Operations
Related Topics:
decimals, fractals, fractions, geometric sequences, geometry, iteration, length, pattern, self-similarity, sequences, surface area, symmetry
Step through the generation of a Hilbert Curve -- a fractal made from deforming a line by bending it, and explore number patterns in sequences and geometric properties of fractals.
Audiences:
Grades 3-5, Grades 6-8, Grades 9-12
Primary Subjects:
Discrete, Fractions, Geometry, Number and Operations
Related Topics:
chaos, fractals, geometric sequences, geometry, iteration, length, lines, pattern, recursion, self-similarity, sequences
Step through the generation of the Koch Snowflake -- a fractal made from deforming the sides of a triangle, and explore number patterns in sequences and geometric properties of fractals.
Audiences:
Grades 3-5, Grades 6-8, Grades 9-12, Undergraduate
Primary Subjects:
Discrete, Fractions, Geometry, Number and Operations
Related Topics:
decimals, fractals, geometric sequences, infinity, iteration, lines, pre-calculus, recursion, self-similarity, sequences
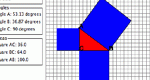
Calculate the length of one side of an automatically generated right triangle by using the Pythagorean Theorem, and then check your answers. Pythagorean Explorer is one of the Interactivate assessment explorers.
Audiences:
Grades 6-8, Grades 9-12
Primary Subjects:
Geometry, Trigonometry
Related Topics:
algebra, angles, assessment, distance, exponents, geometry, length, pythagorean theorem, solving equations, squares, triangle, trigonometry
Step through the generation of Sierpinski's Carpet -- a fractal made from subdividing a square into nine smaller squares and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.
Audiences:
Grades 3-5, Grades 6-8, Grades 9-12
Primary Subjects:
Discrete, Fractions, Geometry, Number and Operations
Related Topics:
algebra, area, fractals, fractions, geometric sequences, iteration, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences
Step through the generation of Sierpinski's Triangle -- a fractal made from subdividing a triangle into four smaller triangles and cutting the middle one out. Explore number patterns in sequences and geometric properties of fractals.
Audiences:
Grades 3-5, Grades 6-8, Grades 9-12
Primary Subjects:
Discrete, Fractions, Geometry, Number and Operations
Related Topics:
dimension, fractals, fractions, geometric sequences, geometry, iteration, length, pattern, pre-calculus, recursion, recursive functions, self-similarity, sequences, symmetry, triangle
Learn about how the Pythagorean Theorem works through investigating the standard geometric proof. Parameters: Sizes of the legs of the triangle.
Audiences:
Grades 6-8, Grades 9-12
Primary Subjects:
Geometry, Trigonometry
Related Topics:
algebra, angles, area, coordinate plane, distance, geometry, length, pythagorean theorem, slides, solving equations, squares, triangle, triangles, trigonometry