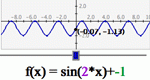These tools listed below are designed such that they can be used as stand-alone applications in analyzing or organizing numbers and data. They are a subset of the activities.
Algebra (22)
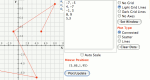
Build your own polygon and transform it in the Cartesian coordinate system. Experiment with reflections across any line, revolving around any line (which yields a 3-D image), rotations about any point, and translations in any direction.
Create your own affine cipher for encoding and decoding messages. Input your own constant and multiplier, then input a message to encode.
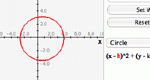
Manipulate different types of conic section equations on a coordinate plane using slider bars. Learn how each constant and coefficient affects the resulting graph. Choose from vertical or horizontal parabola, circle, ellipse, and vertical or horizontal hyperbola.
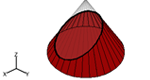
Explore cross sections of different geometric solids: cone, double cone, cylinder, pyramid, and prism. Manipulate the cross section with slider bars, and see how the graphical representation changes.
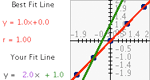
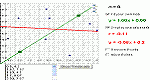
Enter a set of data points, then derive a function to fit those points. Manipulate the function on a coordinate plane using slider bars. Learn how each constant and coefficient affects the resulting graph.
View the graph and the equation of the line tangent to any function at any point on the function.
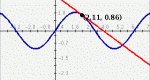
A more advanced version of Slope Slider, this activity allows the manipulation of the constants and coefficients in any function thereby encouraging the user to explore the effects on the graph of the function by changing those numbers.
Students can create graphs of functions entered as algebraic expressions -- similar to a graphing calculator.
Create graphs of functions and sets of ordered pairs on the same coordinate plane. This is like a graphing calculator with advanced viewing options.
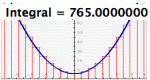
InteGreat! allows the user to visually explore the idea of integration through approximating the integral value with partitions. The user controls the number of partitions, the upper and lower limits, and the method used to estimate the integral.
Enter a set of data points and a function or multiple functions, then manipulate those functions to fit those points. Manipulate the function on a coordinate plane using slider bars. Learn how each constant and coefficient affects the resulting graph.
Students compare multiple independent variables as predictors of one dependent variable. Students explore correlation and lines of best-fit.
Plot ordered pairs on the graph, and they will be connected in the order that they are input. This enables you to decide how the pairs should be connected, rather than having the computer connect them from left to right.
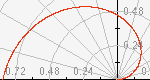
This activity allows the user to explore the polar coordinate system. The applet is similar to GraphIt, but instead allows users to explore the representation of a function in the polar coordinate system.
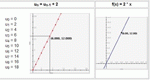
Graph recursive functions by defining f(0)=C and defining f(n) based on f(n-1).
Plot a bivariate data set, determine the line of best fit for their data, and then check the accuracy of your line of best fit.
Graph ordered pairs and customize the graph title and axis labels. Points are connected from left to right, rather than being connected in the order they are entered.
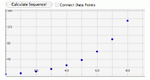
Learn about number patterns in sequences and recursions by specifying a starting number, multiplier, and add-on. The numbers in the sequence are displayed on a graph, and they are also listed below the graph.
Plot ordered pairs of numbers, either as a scatter plot or with the dots connected. Points are connected from right to left, rather than being connected in the order they are entered.
Similar to other "flyers", Slope Slider uses slider bars to explore the effect of the multiplier and constant on a linear function of the form f(x)=mx+b. Explore the relationship between slope and intercept in the Cartesian coordinate system.
Enter two complex numbers (z and c) as ordered pairs of real numbers, then click a button to iterate step by step. The iterates are graphed in the x-y plane and printed out in table form. This is an introduction to the idea of prisoners/escapees in iterated functions and the calculation of fractal Julia sets.
Students create linear inequalities and systems of linear inequalities on a coordinate plane. This is like a graphing calculator with advanced viewing options.
Calculus (12)
Build your own polygon and transform it in the Cartesian coordinate system. Experiment with reflections across any line, revolving around any line (which yields a 3-D image), rotations about any point, and translations in any direction.
Explore cross sections of different geometric solids: cone, double cone, cylinder, pyramid, and prism. Manipulate the cross section with slider bars, and see how the graphical representation changes.
View the graph and the equation of the line tangent to any function at any point on the function.
A more advanced version of Slope Slider, this activity allows the manipulation of the constants and coefficients in any function thereby encouraging the user to explore the effects on the graph of the function by changing those numbers.
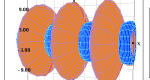
This activity allows the user to find the volume and surface area of various functions as they are rotated around axes. This applet can be used to practice finding integrals using the disk and washer methods of calculating volume.
Students can create graphs of functions entered as algebraic expressions -- similar to a graphing calculator.
Create graphs of functions and sets of ordered pairs on the same coordinate plane. This is like a graphing calculator with advanced viewing options.
InteGreat! allows the user to visually explore the idea of integration through approximating the integral value with partitions. The user controls the number of partitions, the upper and lower limits, and the method used to estimate the integral.
Enter a set of data points and a function or multiple functions, then manipulate those functions to fit those points. Manipulate the function on a coordinate plane using slider bars. Learn how each constant and coefficient affects the resulting graph.
This activity allows the user to plot ordered pairs and parametric equations on the same coordinate plane. The applet is similar to GraphIt, but instead allows users to explore the parametric representation of a function.
This activity allows the user to explore the polar coordinate system. The applet is similar to GraphIt, but instead allows users to explore the representation of a function in the polar coordinate system.
Plot a bivariate data set, determine the line of best fit for their data, and then check the accuracy of your line of best fit.
Discrete (11)
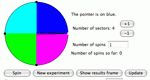
Create a game spinner with variable sized sectors to look at experimental and theoretical probabilities. Parameters: Sizes of sectors, number of sectors, number of trials.
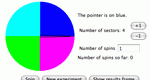
Create a game spinner with one to twelve sectors in order to look at experimental and theoretical probabilities. Parameters: Number of sectors, number of trials.
Create your own affine cipher for encoding and decoding messages. Input your own constant and multiplier, then input a message to encode.
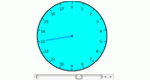
Work with various types of clocks in order to learn about modular arithmetic operations. Parameters: Number of hours on the clock.
Experiment with probability using a fixed size section spinner, a variable section spinner, two regular 6-sided dice or customized dice.
Generate complicated geometric fractals by specifying starting polygon and scale factor.
Enter a complex value for "c" in the form of an ordered pair of real numbers. The applet draws the fractal Julia set for that seed value.
Visually explore counting and place value with different number bases, from base 2 to base 16, and up to the hundreds place using a clock like interface. The activity also allows you to look at the numbers on the clock in base 10 or in your other chosen base to explore the relationship between those values.
Graph recursive functions by defining f(0)=C and defining f(n) based on f(n-1).
Learn about number patterns in sequences and recursions by specifying a starting number, multiplier, and add-on. The numbers in the sequence are displayed on a graph, and they are also listed below the graph.
Explore fractals by investigating the relationships between the Mandelbrot set and Julia sets.
Fractions (6)
Create a game spinner with variable sized sectors to look at experimental and theoretical probabilities. Parameters: Sizes of sectors, number of sectors, number of trials.
Create a game spinner with one to twelve sectors in order to look at experimental and theoretical probabilities. Parameters: Number of sectors, number of trials.
Enter your own data categories and the value of each category to create a pie chart. There are also built in data sets which can be viewed.
Converts fractions to decimals and decimals to fractions. Observe the relationships between fractions and decimals.
Enter a complex value for "c" in the form of an ordered pair of real numbers. The applet draws the fractal Julia set for that seed value.
Explore fractals by investigating the relationships between the Mandelbrot set and Julia sets.
Geometry (16)
Build your own polygon and transform it in the Cartesian coordinate system. Experiment with reflections across any line, revolving around any line (which yields a 3-D image), rotations about any point, and translations in any direction.
Manipulate different types of conic section equations on a coordinate plane using slider bars. Learn how each constant and coefficient affects the resulting graph. Choose from vertical or horizontal parabola, circle, ellipse, and vertical or horizontal hyperbola.
Explore cross sections of different geometric solids: cone, double cone, cylinder, pyramid, and prism. Manipulate the cross section with slider bars, and see how the graphical representation changes.
Create your own fractals by drawing a "line deformation rule" and stepping through the generation of a geometric fractal. Parameters: Grid type, number of bending points on the line.
Build a "floor tile" by dragging the corners of a quadrilateral. Learn about tessellation of quadrilateral figures when the shape you built is tiled over an area.
Generate complicated geometric fractals by specifying starting polygon and scale factor.
Measure angles, distances, and areas in several different images (choices include maps, aerial photos, and others). A scale feature allows the user to set the scale used for measuring distances and areas.
Enter a complex value for "c" in the form of an ordered pair of real numbers. The applet draws the fractal Julia set for that seed value.
Plot ordered pairs on the graph, and they will be connected in the order that they are input. This enables you to decide how the pairs should be connected, rather than having the computer connect them from left to right.
Plot ordered pairs of numbers, either as a scatter plot or with the dots connected. Points are connected from right to left, rather than being connected in the order they are entered.
Functions like a real stopwatch, recording times that you choose. This stopwatch is accurate to the nearest tenth of a second. Parameters: Count up from 0 or count down from a set time.
Create a tessellation by deforming a triangle, rectangle or hexagon to form a polygon that tiles the plane. Corners of the polygons may be dragged, and corresponding edges of the polygons may be dragged. Parameters: Colors, starting polygon.
Explore fractals by investigating the relationships between the Mandelbrot set and Julia sets.
Explore the world of translations, reflections, and rotations in the Cartesian coordinate system by transforming squares, triangles and parallelograms. Parameters: Shape, x or y translation, x or y reflection, angle of rotation.
Build your own polygon and transform it in the Cartesian coordinate system. Experiment with reflections across any line, rotations about any point, and translations in any direction. Parameters: Shape, x or y translation, x or y reflection, angle of rotation
Enter two complex numbers (z and c) as ordered pairs of real numbers, then click a button to iterate step by step. The iterates are graphed in the x-y plane and printed out in table form. This is an introduction to the idea of prisoners/escapees in iterated functions and the calculation of fractal Julia sets.
Graphs (28)
Build your own polygon and transform it in the Cartesian coordinate system. Experiment with reflections across any line, revolving around any line (which yields a 3-D image), rotations about any point, and translations in any direction.
Enter data to create a bar graph, then change many settings for the graph's appearance.
Students can create box plots for either built-in or user-specified data as well as experiment with outliers. User may choose to use or not use the median for calculation of interquartile range.
Enter your own data categories and the value of each category to create a pie chart. There are also built in data sets which can be viewed.
Manipulate different types of conic section equations on a coordinate plane using slider bars. Learn how each constant and coefficient affects the resulting graph. Choose from vertical or horizontal parabola, circle, ellipse, and vertical or horizontal hyperbola.
Explore cross sections of different geometric solids: cone, double cone, cylinder, pyramid, and prism. Manipulate the cross section with slider bars, and see how the graphical representation changes.
Enter a set of data points, then derive a function to fit those points. Manipulate the function on a coordinate plane using slider bars. Learn how each constant and coefficient affects the resulting graph.
A more advanced version of Slope Slider, this activity allows the manipulation of the constants and coefficients in any function thereby encouraging the user to explore the effects on the graph of the function by changing those numbers.
Students can create graphs of functions entered as algebraic expressions -- similar to a graphing calculator.
Create graphs of functions and sets of ordered pairs on the same coordinate plane. This is like a graphing calculator with advanced viewing options.
View histograms for built-in or user-specified data. Experiment with how the size of the class intervals influences the appearance of the histogram. Parameters: Data sets, class sizes.
InteGreat! allows the user to visually explore the idea of integration through approximating the integral value with partitions. The user controls the number of partitions, the upper and lower limits, and the method used to estimate the integral.
Enter data to create a double bar graph, then manipulate the graph's maximum and minimum values.
Change the standard deviation of an automatically generated normal distribution to create a new histogram. Observe how well the histogram fits the curve, and how areas under the curve correspond to the number of trials. Parameters: standard deviation, number of trials, class intervals.
Plot ordered pairs on the graph, and they will be connected in the order that they are input. This enables you to decide how the pairs should be connected, rather than having the computer connect them from left to right.
Create a pie chart, adjusting the size of the divisions using your mouse or by entering values. Parameters: Number of sections, size of sections, whether to use percents or fractions.
PlopIt allows users to build dot plots of data using the mouse. View how the mean, median, and mode change as entries are added to the plot. Parameters: Range for observations.
This activity allows the user to explore the polar coordinate system. The applet is similar to GraphIt, but instead allows users to explore the representation of a function in the polar coordinate system.
Graph recursive functions by defining f(0)=C and defining f(n) based on f(n-1).
Plot a bivariate data set, determine the line of best fit for their data, and then check the accuracy of your line of best fit.
Graph ordered pairs and customize the graph title and axis labels. Points are connected from left to right, rather than being connected in the order they are entered.
Learn about number patterns in sequences and recursions by specifying a starting number, multiplier, and add-on. The numbers in the sequence are displayed on a graph, and they are also listed below the graph.
Plot ordered pairs of numbers, either as a scatter plot or with the dots connected. Points are connected from right to left, rather than being connected in the order they are entered.
Change the median and standard deviation of an automatically generated normal distribution to create a skewed distribution, allowing you to observe properties like what it means for the mean, median, and mode to be different. Parameters: median, standard deviation, number of trials, class intervals.
Similar to other "flyers", Slope Slider uses slider bars to explore the effect of the multiplier and constant on a linear function of the form f(x)=mx+b. Explore the relationship between slope and intercept in the Cartesian coordinate system.
Explore the world of translations, reflections, and rotations in the Cartesian coordinate system by transforming squares, triangles and parallelograms. Parameters: Shape, x or y translation, x or y reflection, angle of rotation.
Build your own polygon and transform it in the Cartesian coordinate system. Experiment with reflections across any line, rotations about any point, and translations in any direction. Parameters: Shape, x or y translation, x or y reflection, angle of rotation
Enter two complex numbers (z and c) as ordered pairs of real numbers, then click a button to iterate step by step. The iterates are graphed in the x-y plane and printed out in table form. This is an introduction to the idea of prisoners/escapees in iterated functions and the calculation of fractal Julia sets.
Modeling (3)
Enter a set of data points, then derive a function to fit those points. Manipulate the function on a coordinate plane using slider bars. Learn how each constant and coefficient affects the resulting graph.
Enter a set of data points and a function or multiple functions, then manipulate those functions to fit those points. Manipulate the function on a coordinate plane using slider bars. Learn how each constant and coefficient affects the resulting graph.
Students compare multiple independent variables as predictors of one dependent variable. Students explore correlation and lines of best-fit.
Number and Operations (10)
Create your own affine cipher for encoding and decoding messages. Input your own constant and multiplier, then input a message to encode.
Work with various types of clocks in order to learn about modular arithmetic operations. Parameters: Number of hours on the clock.
Converts fractions to decimals and decimals to fractions. Observe the relationships between fractions and decimals.
Create your own fractals by drawing a "line deformation rule" and stepping through the generation of a geometric fractal. Parameters: Grid type, number of bending points on the line.
Enter a complex value for "c" in the form of an ordered pair of real numbers. The applet draws the fractal Julia set for that seed value.
Visually explore counting and place value with different number bases, from base 2 to base 16, and up to the hundreds place using a clock like interface. The activity also allows you to look at the numbers on the clock in base 10 or in your other chosen base to explore the relationship between those values.
Graph recursive functions by defining f(0)=C and defining f(n) based on f(n-1).
Learn about number patterns in sequences and recursions by specifying a starting number, multiplier, and add-on. The numbers in the sequence are displayed on a graph, and they are also listed below the graph.
Explore fractals by investigating the relationships between the Mandelbrot set and Julia sets.
Enter two complex numbers (z and c) as ordered pairs of real numbers, then click a button to iterate step by step. The iterates are graphed in the x-y plane and printed out in table form. This is an introduction to the idea of prisoners/escapees in iterated functions and the calculation of fractal Julia sets.
Probability (4)
Create a game spinner with variable sized sectors to look at experimental and theoretical probabilities. Parameters: Sizes of sectors, number of sectors, number of trials.
Create a game spinner with one to twelve sectors in order to look at experimental and theoretical probabilities. Parameters: Number of sectors, number of trials.
Experiment with probability using a fixed size section spinner, a variable section spinner, two regular 6-sided dice or customized dice.
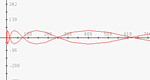
In this applet you can adjust the parameters on two Gaussian curves to determine if there is a possibility of a difference between the two means.
Science (0)
Statistics (23)
Create a game spinner with variable sized sectors to look at experimental and theoretical probabilities. Parameters: Sizes of sectors, number of sectors, number of trials.
Enter data to create a bar graph, then change many settings for the graph's appearance.
Create a game spinner with one to twelve sectors in order to look at experimental and theoretical probabilities. Parameters: Number of sectors, number of trials.
Students can create box plots for either built-in or user-specified data as well as experiment with outliers. User may choose to use or not use the median for calculation of interquartile range.
Enter your own data categories and the value of each category to create a pie chart. There are also built in data sets which can be viewed.
Enter a set of data points, then derive a function to fit those points. Manipulate the function on a coordinate plane using slider bars. Learn how each constant and coefficient affects the resulting graph.
Experiment with probability using a fixed size section spinner, a variable section spinner, two regular 6-sided dice or customized dice.
This applet allows the user to experiment with randomly generated data sets at various sample sizes and standard deviations. Then, users can compare the distribution of the experimental data to the expected distribution.
Create graphs of functions and sets of ordered pairs on the same coordinate plane. This is like a graphing calculator with advanced viewing options.
View histograms for built-in or user-specified data. Experiment with how the size of the class intervals influences the appearance of the histogram. Parameters: Data sets, class sizes.
Enter data and view the mean, median, variance, and standard deviation of the data set. Parameters: Number of observations, range for observations, which statistics to view, identifiers for the data.
Enter data to create a double bar graph, then manipulate the graph's maximum and minimum values.
Enter a set of data points and a function or multiple functions, then manipulate those functions to fit those points. Manipulate the function on a coordinate plane using slider bars. Learn how each constant and coefficient affects the resulting graph.
Students compare multiple independent variables as predictors of one dependent variable. Students explore correlation and lines of best-fit.
Change the standard deviation of an automatically generated normal distribution to create a new histogram. Observe how well the histogram fits the curve, and how areas under the curve correspond to the number of trials. Parameters: standard deviation, number of trials, class intervals.
Plot ordered pairs on the graph, and they will be connected in the order that they are input. This enables you to decide how the pairs should be connected, rather than having the computer connect them from left to right.
In this applet you can adjust the parameters on two Gaussian curves to determine if there is a possibility of a difference between the two means.
Create a pie chart, adjusting the size of the divisions using your mouse or by entering values. Parameters: Number of sections, size of sections, whether to use percents or fractions.
PlopIt allows users to build dot plots of data using the mouse. View how the mean, median, and mode change as entries are added to the plot. Parameters: Range for observations.
Plot a bivariate data set, determine the line of best fit for their data, and then check the accuracy of your line of best fit.
Graph ordered pairs and customize the graph title and axis labels. Points are connected from left to right, rather than being connected in the order they are entered.
Plot ordered pairs of numbers, either as a scatter plot or with the dots connected. Points are connected from right to left, rather than being connected in the order they are entered.
Change the median and standard deviation of an automatically generated normal distribution to create a skewed distribution, allowing you to observe properties like what it means for the mean, median, and mode to be different. Parameters: median, standard deviation, number of trials, class intervals.
Trigonometry (6)
Enter a set of data points, then derive a function to fit those points. Manipulate the function on a coordinate plane using slider bars. Learn how each constant and coefficient affects the resulting graph.
A more advanced version of Slope Slider, this activity allows the manipulation of the constants and coefficients in any function thereby encouraging the user to explore the effects on the graph of the function by changing those numbers.
Students can create graphs of functions entered as algebraic expressions -- similar to a graphing calculator.
Create graphs of functions and sets of ordered pairs on the same coordinate plane. This is like a graphing calculator with advanced viewing options.
Enter a set of data points and a function or multiple functions, then manipulate those functions to fit those points. Manipulate the function on a coordinate plane using slider bars. Learn how each constant and coefficient affects the resulting graph.
This activity allows the user to explore the polar coordinate system. The applet is similar to GraphIt, but instead allows users to explore the representation of a function in the polar coordinate system.