Flake Maker

What is Flake Maker?

This activity allows the user to build custom line deformation fractals.

Line deformation fractals are interesting examples of a recursive process. Here we start with a line and bend it into a series of connected line segments. One can generate regular and irregular fractals this way.

Here is an example of a regular fractal. The line will be divided into four equal-length line segments and bent as:

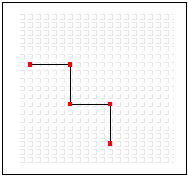
Now the recursive process kicks in: To go to the next stage, each individual line segment is replaced with a scaled copy of the original deformation:

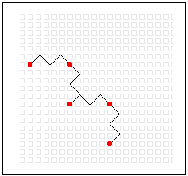
Repeat this process over and over. As the number of stages goes to infinity, a fractal is born. Our eyes can't differentiate really small segments, so we can usually get a good idea of what the fractal would look like after about 5 stages:

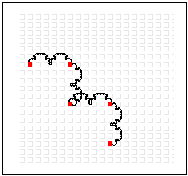
We can also make irregular fractals by breaking the original line into unequal line segments. Here's one:

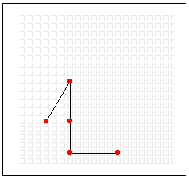
One stage later:

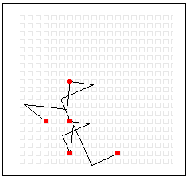
Five stages later:

Related Resources

• Activity Fractured Pictures
• Discussion about Dimension for Irregular Fractals
• Discussion about Recursion
• Discussion about Self-Similarity
• Worksheet Flake Maker Exploration Questions
• Worksheet Flake Maker Exploration Questions (doc)

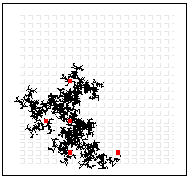
How Do I Use This Activity?

This activity allows the user to build custom line deformation fractals.

Controls and Output

• The Drawing Area at the top of the applet is where the fractal is drawn.

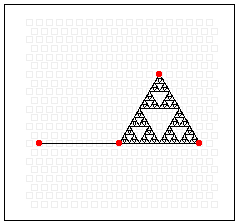
  By moving the red dots on the screen you can manually define how the fractal will be drawn. As you move the red dots the applet will show how the fractal will look. However if you modify the step number so it takes a while for the fractal to draw when you move the dots the image shown will be a simpler version of the fractal that will be drawn when you let go of the dot.

• The Down One and Up One buttons control how many steps of the fractal the applet draws. You can also select the number of steps from the drop-down box between these two buttons.
• You can choose from two types of grids: a Square Grid or a Triangular Grid. The difference between these two grid modes is that the place where you can place the red dots is different. On the Square Grid the location of the points that the red dots can be put in are aranged in a square while on the Triangle Grid they appear more like a triangle. Therefore the Square Grid is easier to use when drawing square-like figures while the Triangle Grid is preferable for Triangles.
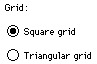
• From the Points box you define the number of red dots you want to appear on the drawing are above.
• The Reset button lines up all the dots the center of the drawing area and clears the fractal you were working on so you can start a new fractal.
• This version of Snowflake is somewhat limited. You can play an Advanced Version by clicking the Go to full version button.

Description

This activity allows the user to generate interesting, irregular fractals. This activity would work well in mixed ability groups of two or three for about twenty-five to thirty minutes if you use the exploration questions and fifteen minutes otherwise.

Place in Mathematics Curriculum

This activity can be used to:

• Practice students' pattern recognition skills
• Practice students' plane geometry skills
• Illustrate the ideas of self-similarity and recursion
• Demonstrate fractal objects

Be Prepared to

• Give implicit directions on what they are to do. For example, "Today we are going to discover how to make fractals using ..."
• Discuss fractions and symmetry.

Related Resources

• Activity Fractured Pictures
• Discussion about Dimension for Irregular Fractals
• Discussion about Recursion
• Discussion about Self-Similarity
• Lesson on Introduction to Fractals: Geometric Fractals
• Lesson on Introduction to Fractals: Infinity, Self-Similarity and Recursion
• Lesson on Irregular Fractals
• Worksheet Flake Maker Exploration Questions
• Worksheet Flake Maker Exploration Questions (doc)