What is Fractured Pictures?
This activity allows the user to generate interesting, irregular fractals.
These fractal objects are made by starting with a polygon, such as a triangle or square -- input by the user as number of sides -- and a fractal scale factor -- also input by the user. The program then draws the figure by recreating in a scaled copy of the original figure at each vertex with some additional embellishments. This process can be repeated for any number of iterations as specified by the user.
Regular fractals can be made from this program as well. Inputs of sides = 3 and scale factor = 2 gives:

Other interesting fractals can be made by varying the inputs; here's sides = 6 and scale = 4:

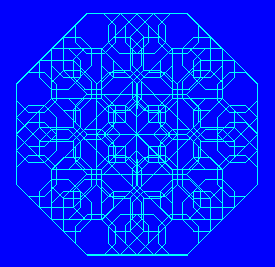
Here's sides = 8 and scale = 3.
How Do I Use This Activity?
This activity allows the user to generate interesting, irregular fractals.
Controls and Output
-
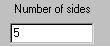
The
Number of Sides input specifies the number of sides of the base regular polygon. 3 is a triangle, 4 is a
square, and so on. Any value from 3 to 100 is acceptable.
-
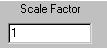
The
Scale Factor input specifies the scale for reducing the size of the polygon in each iteration.
-
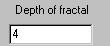
The
Depth of Fractal input specifies the number of iterations to be drawn.
Note that the depth of fractal is dependent on the computing power of the fractal. Thus, high numbers might overwhelm your computer and cause it to freeze. Generally, a depth of 7 or 8 will be your computational limit.
-
The Length of Each Side input specifies the length of each side of the base polygon in screen pixels.
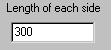
To fit the entire figure into the window, use these guidelines:
Then change the length of the side up and down to zoom in and out on the middle of the figure.Sides = 3 to 10 10 to 50 50 to 100 Length = 100 20 10 -
Once you have input the number of sides, the length of each side, the scale factor, and the depth of the fractal, use the Create Fractal! button to draw the fractal.
Description
This activity allows the user to generate interesting, irregular fractals. This activity would work well in mixed ability groups of two or three for about twenty-five to thirty minutes if you use the exploration questions and fifteen minutes otherwise.
Place in Mathematics Curriculum
This activity can be used to:
- practice students' pattern recognition skills
- practice students' plane geometry skills
- practice students' reasoning and deduction skills
- illustrate the ideas of self-similarity and recursion
- demonstrate fractal objects
Standards Addressed
Grade 6
-
Geometry
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
Grade 7
-
Geometry
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
Grade 8
-
Geometry
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
Grade 9
-
Geometry
- The student demonstrates an understanding of geometric relationships.
- The student demonstrates a conceptual understanding of geometric drawings or constructions.
Grade 10
-
Geometry
- The student demonstrates an understanding of geometric relationships.
- The student demonstrates a conceptual understanding of geometric drawings or constructions.
Number and Quantity
-
Quantities
- Reason quantitatively and use units to solve problems.
Grades 9-12
-
Geometry
- Use visualization, spatial reasoning, and geometric modeling to solve problems
Geometry
-
Geometry and Measurement
- Competency Goal 2: The learner will use geometric and algebraic properties of figures to solve problems and write proofs.
Technical Mathematics I
-
Geometry and Measurement
- Competency Goal 2: The learner will measure and apply geometric concepts to solve problems.
Technical Mathematics II
-
Geometry and Measurement
- Competency Goal 1: The learner will use properties of geometric figures to solve problems.
Advanced Functions and Modeling
-
Algebra
- Competency Goal 2: The learner will use functions to solve problems.
Discrete Mathematics
-
Algebra
- Competency Goal 3: The learner will describe and use recursively-defined relationships to solve problems.
Integrated Mathematics III
-
Geometry and Measurement
- Competency Goal 2: The learner will use properties of geometric figures to solve problems.
Be Prepared to
- give implicit directions on what they are to do. For example, "Today we are going to discover how to make fractals using ..."
- discuss fractions and symmetry