Number Base Clocks

What is Number Base Clocks?

This activity allows you to convert between a number in a different base and base ten. The number system we are used to working in is called base 10 because there are ten digits, 0 though 9. In a base 7 number system, there would be 7 digits 0 through 6.

In a base 12 number system there would be twelve individual digits representing the values 0 through 11. Often, with number systems greater than ten, we start using digits from the alphabet and thus, 10 and 11 would be represented with A and B respectively.

The ancient Mayans used base 20 as their counting system and the Sumerians used base 60. Computer scientists often have to use base 2 as well as base 16. Most people today use base 10. Trying to do calculations with hours and minutes or feet and inches is also similar to calculating in base 60 or base 12.

Related Resources

• Activity Clock Arithmetic
• Discussion about Base Ten
• Discussion about Clocks and Modular Arithmetic
• Discussion about Converting From Base Ten
• Discussion about Place Value
• Worksheet Number Base Clocks Exploration Questions
• Worksheet Number Base Clocks Exploration Questions (doc)

How Do I Use This Activity?

This activity can be used to understand other number bases. The user can enter a number and calculate that number with a different base value. The answer is displayed on three clocks, one for each digit and below them in numerical form.

Controls and Output

The slider bar at the top left-hand side of the activity allows you to adjust the base value. The default is base 10 and the minimum is base 2 and the maximum is base 16.

Opposite from the slider bar is a textbox where you can enter the base ten number you want to calculate in another base. You must enter a number greater than or equal to zero and the maximum number you can enter changes depending on the base value. The maximum value (in base 10) is the base minus one times the base squared.

Once you have entered the number, click one of the two buttons next to it that say either 'step' or 'count'. Once you have clicked 'count', the button becomes a 'stop' button and you may click this to stop the calculation and animation.

'Count' will begin the calculation and animation of the clocks. Use the animation drop down menu to select how quickly the clock is animated. Choose from fast, medium, and slow, or choose "Do not animate" if you want to see the result but not watch the animation.

'Step' also begins the calculation, but allows you to see the animation step by step.

The two equations below the clocks show you how the number you entered is calculated in the base value you specified on the left, and how it is calculated in base 10 on the right.

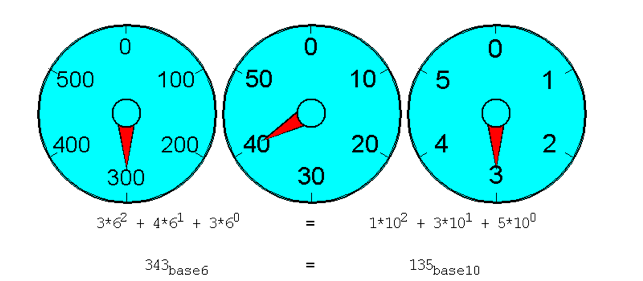
Each clock corresponds to a term in the left equation. The values on the clock indicate the possible values that each term can contribute to the answer you see in front of the base (in this case 343). Thus, the right most term, in this example can contribute 0, 1, 2 ,3, 4 or 5 (it contributes 3 here) to the final answer.

You can view the values on the clock in your chosen base rather than in base 10 by un-checking the box next to 'Number Clocks in Base 10'.

If you wish to enter another value after you have already entered one, click 'Reset'.

Description

This activity allows the user to experiment with converting from base 10 to other base values, up to base 16. This activity would work well in groups for about 45 minutes if you use the exploration questions and about 15 minutes otherwise.

Place in Mathematics Curriculum

This activity can be used to:

• Understand modular arithmetic
• Introduce the idea of systems other than base 10
• Learn how to convert from base 10 to other bases
• Practice long division and dealing with remainders

Be Prepared to

• Explain what a "base" is
• Demonstrate how to convert a number in base 10 into a number in another base by hand
• Explain the difference between numbering the clocks in base 10 and not numbering them in base 10
• Answer the question, "Why do some of the clocks have letters on them?"
• Answer the question, "Why do some bases have four clocks and some only have three?"

Related Resources

• Activity Clock Arithmetic
• Discussion about Base Ten
• Discussion about Clocks and Modular Arithmetic
• Discussion about Converting From Base Ten
• Discussion about Place Value
• Lesson on Clock Arithmetic and Cryptography
• Lesson on Modular Arithmetic
• Lesson on Number Base Clocks
• Worksheet Number Base Clocks Exploration Questions
• Worksheet Number Base Clocks Exploration Questions (doc)