Clock Arithmetic

What is Clock Arithmetic?

Clock time can be thought of as a type of modular arithmetic. Modular arithmetic is used when we only want to consider the first N natural numbers, for some finite number N. There are two cases to consider when we add or multiply numbers in this situation:

1. When we add or multiply two numbers and the result is less than N, the final answer is just the number resulting from the addition or multiplication.
2. When we add or multiply two numbers and the result is more than N, the final answer is found by thinking of the numbers as looping back to the beginning, i.e., N = 0, N + 1 = 1, N + 2 = 2, etc.

We can think of clocks this way. For our usual clock, we think of the typical dial, except with 12 = 0. So 13 hours after 0 o'clock is 1 o'clock (13 = 12+1 which is 1 on the dial).

A clock with 5 hours works the same way: 17 hours after 0 o'clock is 2 o'clock (17 = 5 + 12 = 10 + 7 = 15 + 2 which is 2 on the dial).

Related Resources

• Activity Arithmetic Four
• Activity Arithmetic Quiz
• Activity Caesar Cipher
• Activity Caesar Cipher II
• Activity Caesar Cipher III
• Activity Elapsed Time
• Activity Number Base Clocks
• Discussion about Clocks and Modular Arithmetic
• Discussion about Cryptography and Ciphers
• Discussion about What are Multiples
• Discussion about What are Remainders
• Worksheet Clock Arithmetic Exploration Questions
• Worksheet Clock Arithmetic Exploration Questions (doc)

How Do I Use This Activity?

This activity can be used to explore modular arithmetic. The user sets a starting value and then moves the "clock" forward a number of specified hours to see the resulting sum. The activity also displays the number of times the "clock" passes the starting value.

Controls and Output

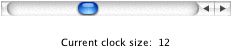
• You can use the scrollbar to modify the size of the clock. The clock's size ranges from 2 to 26. In the example below, the current clock size is 12.

• After you have set the clock to the size you want, you can enter the number of the hour of where you want the clock to start. This number can be anywhere between 0 and one less than the size of the clock. For example, if the clock size was 12, the starting time could range from 0 and 11. An example of entering a starting time of 0:

  After you enter the starting time, press on the button. This will move the clock hand to the number you input:

  

  Also, the place where you entered the starting time should turn grey and will no longer be editable:

  

  A message should then appear in the text field:

  

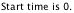
  Use the animation drop down menu to select how quickly the clock is animated. Choose from fast, medium, and slow, or choose "Do not animate" if you want to see the result but not watch the animation.

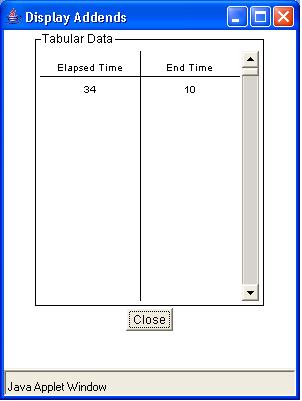
• To make the clock hand move, enter a number into the input for the elapsed time. This number must be between 0 and 1000. An example of entering an elapsed time of 34 hours is:

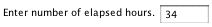
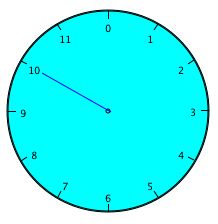
  To make this change on the clock, press on the button. The hand moves forward on the clock the number of hours that you specified. An example of a clock of size 12, which started on time 0 and moved 34 hours:

  

  Also, a message appears in the text field. It gives the start time, the calculated time after the clock moves the elapsed time you specified, and the number of times the hand passed the starting time:

  

• Another option in this applet is to display the addends. This gives a list of elapsed times and end times. These can be viewed by clicking on the button. A pop-up window should appear:
• The button will return the clock hand to the initial zero position and allows you to enter in a new starting time.

Description

This activity allows the user to experiment with clock (modular) arithmetic. This activity would work well in mixed ability groups of two or three for about thirty minutes if you use the exploration questions and fifteen minutes otherwise.

Place in Mathematics Curriculum

This activity can be used to:

• practice students' long division skills
• motivate the ideas of modular arithmetic

Be Prepared to

• explain that not all people use a twelve hour clock.
• explain some of the benefits of military time.

Related Resources

• Activity Arithmetic Four
• Activity Arithmetic Quiz
• Activity Caesar Cipher
• Activity Caesar Cipher II
• Activity Caesar Cipher III
• Activity Elapsed Time
• Activity Number Base Clocks
• Discussion about Clocks and Modular Arithmetic
• Discussion about Cryptography and Ciphers
• Discussion about What are Multiples
• Discussion about What are Remainders
• Lesson on Clock Arithmetic and Cryptography
• Lesson on Finding Remainders in Pascal's Triangle
• Lesson on Modular Arithmetic
• Worksheet Clock Arithmetic Exploration Questions
• Worksheet Clock Arithmetic Exploration Questions (doc)