What is Sequencer?
This activity allows the user to create multiple sequences by varying the following values:
- Starting Number: The first number in the sequence.
- Multiplier: The number by which the preceding element of the sequence will be multiplied.
- Add-on: The number that is added to the preceding number (after it has been multiplied by the multiplier) to obtain the next number in the sequence.
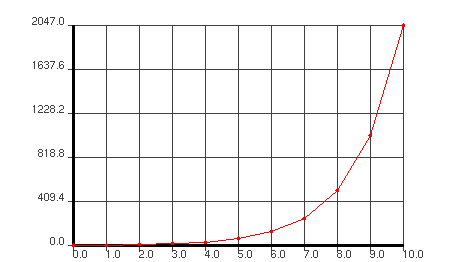
A given element of the sequence is obtained by multiplying the preceding number by the multiplier, and then adding the add-on. A graph of the resulting sequence and a list of the elements of the sequence are displayed in the applet.
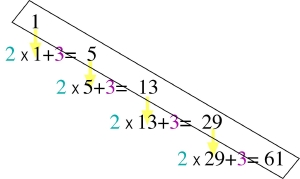
For example, if our starting number is 1, our multiplier is 2 and our add-on is 3, we get the following numbers:
How Do I Use This Activity?
This applet allows the user to create various sequences by inputting a starting number, a multiplier, and an add-on.
Controls and Output
-
First, enter a starting number, a multiplier, and an add-on into the appropriate boxes on
the applet. This applet allows the user to enter integers, decimals, and fractions.
-
Next, click on the button labeled
Calculate Sequence.

-
Below the
Calculate Sequence button you will see a graph displaying the resulting sequence as well as a box containing
the elements of the sequence.
- You may change the initial values at any time and see the resulting sequence by clicking Calculate Sequence.
Description
This activity allows the user to enter a starting number, a multiplier, and an add-on to create sequences. This activity would work well in groups of two or three for about thirty minutes if you use the exploration questions and ten to fifteen minutes otherwise.
Place in Mathematics Curriculum
This activity can be used to:
- introduce sequences
- allow students to create sequences by varying the starting number, multiplier, or add-on
- reinforce previously obtained knowledge regarding the behavior of sequences
- practice computational skills
Standards Addressed
Grade 6
-
Functions and Relationships
- The student demonstrates conceptual understanding of functions, patterns, or sequences.
Grade 7
-
Functions and Relationships
- The student demonstrates conceptual understanding of functions, patterns, or sequences including those represented in real-world situations.
Grade 8
-
Functions and Relationships
- The student demonstrates conceptual understanding of functions, patterns, or sequences including those represented in real-world situations.
Grade 9
-
Functions and Relationships
- The student demonstrates conceptual understanding of functions, patterns, or sequences including those represented in real-world situations.
- The student demonstrates algebraic thinking.
Grade 10
-
Functions and Relationships
- The student demonstrates conceptual understanding of functions, patterns, or sequences including those represented in real-world situations.
- The student demonstrates algebraic thinking.
Functions
-
Linear, Quadratic, and Exponential Models
- Construct and compare linear, quadratic, and exponential models and solve problems
Grades 6-8
-
Numbers and Operations
- Understand meanings of operations and how they relate to one another
Grades 9-12
-
Algebra
- Understand patterns, relations, and functions
- Use mathematical models to represent and understand quantitative relationships
Grade 6
-
Number and Operations, Measurement, Geometry, Data Analysis and Probability, Algebra
- COMPETENCY GOAL 1: The learner will understand and compute with rational numbers.
Grade 7
-
Number and Operations, Measurement, Geometry, Data Analysis and Probability, Algebra
- COMPETENCY GOAL 1: The learner will understand and compute with rational numbers.
Advanced Functions and Modeling
-
Algebra
- Competency Goal 2: The learner will use functions to solve problems.
Discrete Mathematics
-
Algebra
- Competency Goal 3: The learner will describe and use recursively-defined relationships to solve problems.
Pre-Calculus
-
Geometry and Measurement
- Competency Goal 2: The learner will use relations and functions to solve problems.
Pre-Calculus
-
Knowledge and Skills
- 4. The student uses sequences and series as well as tools and technology to represent, analyze, and solve real-life problems.
Be Prepared to
- give implicit directions on what students are to do. For example "Today we are going to experiment with the Sequencer activity..."
- explain what a starting number, multiplier, and add-on are and how they affect the sequence
- answer the question "How does the computer graph the sequence?"