What is Equation Solver?
This activity allows the user to practice solving algebraic equations using the additive and multiplicative inverses.
Solving an algebraic equation means finding the value of an unknown in an equation that will make that equation true. There are many ways to solve algebraic equations. Frequently, solving algebraic equations entails "isolating the variable" using relationships of equality and properties of real numbers such as the distributive property, the associative property, the commutative property, and both the multiplicative inverse and additive inverse. For these equations, you will use the multiplicative and additive inverses to solve for X.
How Do I Use This Activity?
This activity allows the user to practice solving algebraic equations by applying the additive inverse and multiplicative inverse properties. There is also an option to apply the additive identity and multiplicative identity properties.
Controls and Output
-
To begin, choose the difficulty level: Level 1, Level 2, or Level 3.

-
After selecting your difficulty level, an equation will appear in the Equation box.

-
To perform an operation on the equation, the user must first select the
property to apply to the equation.

-
Then the user must choose an operator.

- Note that multiplication and division operations can only be used with the multiplicative inverse and not the additive inverse. Likewise, addition and subtraction operations can only be used with the additive inverse property.
-
Then the user must enter a term. This will be the value the user wishes to add, subtract,
multiply by, or divide to both sides of the equation.

- If the user wants to add or subtract a fraction of x, the user must enter the fraction 1/4, and then the variable x. This will read 1/4x in the text box. The computer will interpret this as "one-fourth x".
-
After doing all of these steps, the user can click the enter button. This will perform the
operation on the equation.

-
Before solving the problem, the user can also choose to
use identity properties, by checking the box at the top:

-
If the user chooses to do this, the
Identity Properties will be included under the property menu:

-
Using the Identity Properties will require the user to take an additional step to remove
the zero in the case of addition and the one in the case of multiplication. See the
example below:

- The user must then repeat this process with other steps until they have solved the problem by isolating x.
- If you ever want to back up and try something different, you can do so by clicking the Back a Step Button. Note that using this button will increase the total number of steps it takes to solve the equation and will affect the overall score if scoring is active.
- You can also start the equation again by clicking the Reset Problem Button. Note that resetting a problem will affect the score by counting the current problem as incorrect if scoring is active.
- If you want to restart the game, you can do so by clicking on the New Game button.
-
This activity will automatically record how successful you are at solving the equations.
To view the score, press the
Show Score button at the bottom of the activity and a pop-up window will appear with the scoreboard.
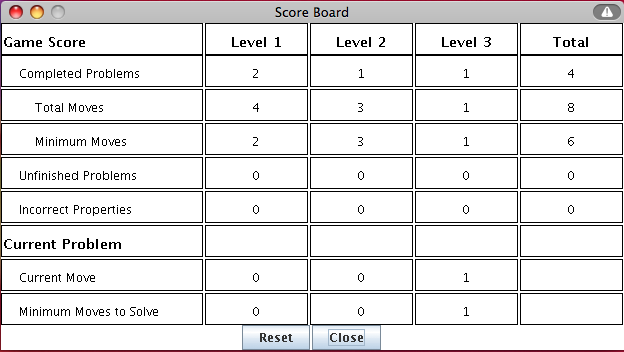
- The information in this window is divided into two sections. The statistics for the current equation are given in the bottom half of the window, and the statistics for all questions together are given in the top half. To close this pop-up window press the Close button or click back on the main window.
- To pause the scoring, press the Active button at the bottom of the screen and it will change to a Paused button. To resume scoring, press the Paused button.
- To reset the scoreboard, open the scoreboard using the Show Score button and then press the Reset button.
Description
This activity allows the user to practice solving algebraic equations using the additive inverse and multiplicative inverse properties. As the user solves the problem, the activity tracks each step, noting the property that was used. This activity would work well in groups of two for about 40 minutes if you use the exploration questions and 20-25 minutes otherwise.
Place in Mathematics Curriculum
This activity can be used to:
- Allow students practice with using the additive and multiplicative inverses to solve algebraic problems.
Standards Addressed
Grade 6
-
Functions and Relationships
- The student demonstrates algebraic thinking.
Grade 7
-
Functions and Relationships
- The student demonstrates algebraic thinking.
Grade 8
-
Functions and Relationships
- The student demonstrates algebraic thinking.
Grade 9
-
Functions and Relationships
- The student demonstrates conceptual understanding of functions, patterns, or sequences including those represented in real-world situations.
- The student demonstrates algebraic thinking.
Grade 10
-
Functions and Relationships
- The student demonstrates conceptual understanding of functions, patterns, or sequences including those represented in real-world situations.
- The student demonstrates algebraic thinking.
Grade 6
-
Algebra and Functions
- 1.0 Students write verbal expressions and sentences as algebraic expressions and equations; they evaluate algebraic expressions, solve simple linear equations, and graph and interpret their results
-
Mathematical Reasoning
- 1.0 Students make decisions about how to approach problems
- 2.0 Students use strategies, skills, and concepts in finding solutions
Grade 7
-
Algebra and Functions
- 1.0 Students express quantitative relationships by using algebraic terminology, expressions, equations, inequalities, and graphs
- 4.0 Students solve simple linear equations and inequalities over the rational numbers
-
Mathematical Reasoning
- 1.0 Students make decisions about how to approach problems
- 2.0 Students use strategies, skills, and concepts in finding solutions
Grades 8-12
-
Algebra I
- 2.0 Students understand and use such operations as taking the opposite, finding the reciprocal, taking a root, and raising to a fractional power. They understand and use the rules of exponents.
- 4.0 Students simplify expressions before solving linear equations and inequalities in one variable, such as 3(2x-5) + 4(x-2) = 12.
- 5.0 Students solve multistep problems, including word problems, involving linear equations and linear inequalities in one variable and provide justification for each step.
Sixth Grade
-
Expressions and Equations
- Apply and extend previous understandings of arithmetic to algebraic expressions.
- Reason about and solve one-variable equations and inequalities.
Seventh Grade
-
Expressions and Equations
- Use properties of operations to generate equivalent expressions.
- Solve real-life and mathematical problems using numerical and algebraic expressions and equations.
Algebra
-
Arithmetic with Polynomials and Rational Expressions
- Perform arithmetic operations on polynomials
- Use polynomial identities to solve problems
- Rewrite rational expressions
-
Reasoning with Equations and Inequalities
- Understand solving equations as a process of reasoning and explain the reasoning
- Solve equations and inequalities in one variable
- Solve systems of equations
Grades 6-8
-
Algebra
- Understand patterns, relations, and functions
-
Numbers and Operations
- Understand meanings of operations and how they relate to one another
Grades 9-12
-
Algebra
- Understand patterns, relations, and functions
-
Numbers and Operations
- Understand meanings of operations and how they relate to one another
Grade 7
-
Number and Operations, Measurement, Geometry, Data Analysis and Probability, Algebra
- COMPETENCY GOAL 5: The learner will demonstrate an understanding of linear relations and fundamental algebraic concepts.
Grade 8
-
Number and Operations, Measurement, Geometry, Data Analysis and Probability, Algebra
- COMPETENCY GOAL 5: The learner will understand and use linear relations and functions.
Introductory Mathematics
-
Algebra
- COMPETENCY GOAL 4: The learner will understand and use linear relations and functions.
Algebra I
-
Algebra
- Competency Goal 4: The learner will use relations and functions to solve problems.
7th Grade
-
Algebra
- The student will demonstrate through the mathematical processes an understanding of proportional relationships.
8th Grade
-
Algebra
- The student will demonstrate through the mathematical processes an understanding of equations, inequalities, and linear functions.
Elementary Algebra
-
Elementary Algebra
- Standard EA-4: The student will demonstrate through the mathematical processes an understanding of the procedures for writing and solving linear equations and inequalities.
8th Grade
-
Algebra
- The student will understand and generalize patterns as they represent and analyze quantitative relationships and change in a variety of contexts and problems using graphs, tables, and equations.
-
Number and Operation
- The student will develop number and operation sense needed to represent numbers and number relationships verbally, symbolically, and graphically and to compute fluently and make reasonable estimates in problem solving.
Algebra I
-
Algebra
- Students will describe, extend, analyze, and create a wide variety of patterns and functions using appropriate materials and representations in real world problem solving.
-
Numbers and Operations
- Students will recognize, represent, model, and apply real numbers and operations verbally, physically, symbolically, and graphically.
Algebra I
-
Foundation for Functions
- 1. The student understands that a function represents a dependence of one quantity on another and can be described in a variety of ways.
- 2. The student uses the properties and attributes of functions.
- 3. The student understands how algebra can be used to express generalizations and recognizes and uses the power of symbols to represent situations.
- 4. The student understands the importance of the skills required to manipulate symbols in order to solve problems and uses the necessary algebraic skills required to simplify algebraic expressions and solve equations and inequalities in problem situations.
-
Linear Functions
- 7. The student formulates equations and inequalities based on linear functions, uses a variety of methods to solve them, and analyzes the solutions in terms of the situation.
7th Grade
-
Number and Number Sense
- 7.3 The student will identify and apply the following properties of operations with real numbers: the commutative and associative properties for addition and multiplication; the distributive property; the additive and multiplicative identity properties; the additive and multiplicative inverse properties; and the multiplicative property of zero.
-
Patterns, Functions, and Algebra
- 7.22a The student will solve one-step linear equations and inequalities in one variable with strategies involving inverse operations and integers, using concrete materials, pictorial representations, and paper and pencil
8th Grade
-
Patterns, Functions, and Algebra
- 8.15 The student will solve two-step equations and inequalities in one variable, using concrete materials, pictorial representations, and paper and pencil.
6th Grade
-
Patterns, Functions, and Algebra
- 6.23b The student will solve one-step linear equations in one variable, involving whole number coefficients and positive rational solutions
Secondary
-
Algebra I
- A.01 The student will solve multistep linear equations and inequalities in one variable, solve literal equations (formulas) for a given variable, and apply these skills to solve practical problems. Graphing calculators will be used to confirm algebraic solutions.
- A.03 The student will justify steps used in simplifying expressions and solving equations and inequalities. Justifications will include the use of concrete objects; pictorial representations; and the properties of real numbers, equality, and inequality.
Textbooks Aligned
Grade Seven
-
Moving Straight Ahead
- Investigation Four: Solving Equations
Grade Eight
-
Say It with Symbols
- Investigation Three: Some Important Properties
- Investigation Four: Solving Equations
Book 3
-
Module 1 - Amazing Feats, Facts and Fictions
- Section 6: Solving Equations
7th
-
Module 1 - Search and Rescue
- Section 5: One-Step Equations
Be Prepared to
- Explain the difference between the additive and multiplicative inverses.
- Explain the additive identity and multiplicative identity properties.
- Encourage students to try more difficult problems and complete problems in the fewest steps possible.