What is Hilbert Curve Generator?
This activity allows the user to step through the generation of a fractal made from deforming a line by bending it. The Hilbert Curve was studied by David Hilbert at the turn of the 20th century as an example 1-dimensional curve filling a 2-dimensional space.
To build a Hilbert curve, start with a line segment 1 unit long. (Iteration 0, or the initiator)
Replace each line segment with the following generator:
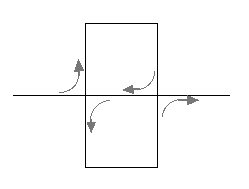
Notice that this replaces a line segment with 9 pieces, all 1/3 the length of the original segment.
Repeat this process on all line segments. Iterations 0, 1, and 2 are shown below.
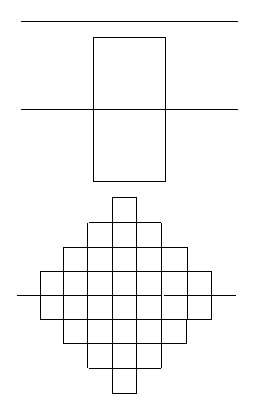
The limit of this process as the number of stages approaches infinity is a Hilbert curve.
The Hilbert Curve is one of the earliest "curious curves" known to have been studied. The Hilbert Curve is the result of repeating a line bending step infinitely many times. Hilbert and Peano were interested in such curves at the end of the 19th century. Many curves of this type were found to be "fractal" in the 1970s.
How Do I Use This Activity?
This activity allows the user to step through the generation of a fractal made from deforming a line by bending it.
Controls and Output
-
The
Next Stage and
Previous Stage buttons at the bottom of the applet control which stage of the fractal is being viewed.

-
The
Output Box at the top of the applet lists the current stage's number of individual line segments and
the individual segment length.

Description
This activity allows the user to step through the process of building a Hilbert curve. This activity would work well in groups of two to four for about twenty minutes if you use the exploration questions and five minutes otherwise.
Place in Mathematics Curriculum
This activity can be used to:
- practice students' fraction manipulation skills
- practice students' pattern finding skills
- demonstrate the complexity of infinity
- motivate the ideas of self-similarity and recursion
- demonstrate fractal objects
- motivate the idea of a limit
Standards Addressed
Grade 6
-
Geometry
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
Grade 7
-
Geometry
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
Grade 8
-
Geometry
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
Grade 9
-
Geometry
- The student demonstrates an understanding of geometric relationships.
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
- The student demonstrates a conceptual understanding of geometric drawings or constructions.
Grade 10
-
Geometry
- The student demonstrates an understanding of geometric relationships.
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
- The student demonstrates a conceptual understanding of geometric drawings or constructions.
Fourth Grade
-
Operations and Algebraic Thinking
- Generate and analyze patterns.
Fifth Grade
-
Operations and Algebraic Thinking
- Analyze patterns and relationships.
Eighth Grade
-
Geometry
- Understand congruence and similarity using physical models, trans- parencies, or geometry software.
Geometry
-
Congruence
- Make geometric constructions
Grades 9-12
-
Algebra
- Represent and analyze mathematical situations and structures using algebraic symbols
- Understand patterns, relations, and functions
-
Measurement
- Apply appropriate techniques, tools, and formulas to determine measurements
Grade 5
-
Number and Operations, Measurement, Geometry, Data Analysis and Probability, Algebra
- COMPETENCY GOAL 1: The learner will understand and compute with non-negative rational numbers.
Grade 6
-
Number and Operations, Measurement, Geometry, Data Analysis and Probability, Algebra
- COMPETENCY GOAL 1: The learner will understand and compute with rational numbers.
Grade 7
-
Number and Operations, Measurement, Geometry, Data Analysis and Probability, Algebra
- COMPETENCY GOAL 1: The learner will understand and compute with rational numbers.
Grade 8
-
Number and Operations, Measurement, Geometry, Data Analysis and Probability, Algebra
- COMPETENCY GOAL 3: The learner will understand and use properties and relationships in geometry.
Introductory Mathematics
-
Data Analysis and Probability
- COMPETENCY GOAL 3: The learner will understand and use properties and relationships in geometry.
-
Geometry and Measurement
- COMPETENCY GOAL 2: The learner will use properties and relationships in geometry and measurement concepts to solve problems.
Geometry
-
Geometry and Measurement
- Competency Goal 2: The learner will use geometric and algebraic properties of figures to solve problems and write proofs.
Technical Mathematics I
-
Geometry and Measurement
- Competency Goal 2: The learner will measure and apply geometric concepts to solve problems.
Technical Mathematics II
-
Geometry and Measurement
- Competency Goal 1: The learner will use properties of geometric figures to solve problems.
Advanced Functions and Modeling
-
Algebra
- Competency Goal 2: The learner will use functions to solve problems.
Discrete Mathematics
-
Algebra
- Competency Goal 3: The learner will describe and use recursively-defined relationships to solve problems.
Integrated Mathematics III
-
Geometry and Measurement
- Competency Goal 2: The learner will use properties of geometric figures to solve problems.
Textbooks Aligned
Grade Six
-
Bits and Pieces I
- Investigation One: Fund-Raising Fractions
- Investigation Two: Comparing Fractions
- Investigation Three: Cooking with Fractions
- Investigation Four: From Fractions to Decimals
- Investigation Five: Moving Between Fractions and Decimals
- Investigation Six: Out of One Hundred
Grade Seven
-
Comparing and Scaling
- Investigation Three: Comparing by Using Ratios
Book 1
-
Module 2 - Patterns and Designs
- Section 2: Fractions
- Section 3: Equivalent Fractions
- Section 5: Decimal Place Value
-
Module 3 - Statistical Safari
- Section 2: Fractions, Percents
- Section 4: Mean, Median, Mode, Averages
-
Module 4 - Mind Games
- Section 3: Fraction Multiplication
-
Module 5 - Creating Things
- Section 1: Common Denominators
- Section 3: Adding Fractions, Subtracting Fractions, Adding Mixed Numbers, Subtracting Mixed Numbers
-
Module 6 - Comparisons and Predictions
- Section 6: Fractions and Percents
Book 2
-
Module 3 - A Universal Language
- Section 2: Comparing Fractions, Adding and Subtracting Fractions
- Section 2: Tree Diagrams and Probability
- Section 4: Integer Exponents
-
Module 4 - The Art of Motion
- Section 1: Multiplying Fractions, Dividing Fractions
-
Module 5 - Recreation
- Section 3: Percents
Book 3
-
Module 2 - At the Mall
- Section 5: Working with Negative Fractions
-
Module 4 - Patterns and Discoveries
- Section 1: Sequences
- Section 1: Fractals
- Section 2: Rational and Irrational Numbers
- Section 3: Equations with Fractions
Book 1
-
From Zero to One and Beyond
- Lesson 1: Folding Fractions
- Lesson 4: Out of One Hundred
- Lesson 5: Percents That Make Sense
- Lesson 9: All Three at Once
-
Number Powerhouse
- Lesson 5: Pluses and Minuses
- Lesson 6: Multiplication Made Easy
- Lesson 7: The Great Fraction Divide
Book 2
-
Buyer Beware
- Lesson 6: Which Brand Has the Most Chocolate?
-
Making Mathematical Arguments
- Lesson 6: Counterexamples and Special Cases
Grade 8
-
Patterns and Figures
- Patterns
- Generalities
- Progressions
- Rectangular Numbers
- Triangular Numbers
- Pascal's Triangle
-
Reflections on Number
- Divisibility and Prime Factorization
- Multiplication and Division
- Operations with Inverses
-
Triangles and Patchwork
- Similarity
- Similar Triangles
- Tessellations
Grade 5
-
Grasping Sizes
- Ratios
- Proportional Enlargements and Reductions
- Scale Lines
- Calculating Ratios
-
Measure for Measure
- Equivalent Decimals
- Fraction/Decimal Equivalence
- Adding and Subtracting Decimals
-
Patterns and Symbols
- Variables
- Patterns
- Pattern Rule
-
Some of the Parts
- Fractions
- Relationships between Fractions
- Operations with Fractions
Grade 6
-
Fraction Times
- Operations with Fractions
- Fraction/Percent/Decimal/Ration Relationships
-
More or Less
- Fraction/Decimal/Percent Relationships
- Operations with Percents
- Decimal Multiplication
-
Ratios and Rates
- Ratio/Fraction/Decimal/Percent Relationships
- Part-Part Ratios
- Part-Whole Ratios
- Scale Factor
- Linear Functions
Grade 7
-
Building Functions
- Algebraic Descriptions
- Sequences
- Equivalent Expressions
- Squares and Square Roots
-
Cereal Numbers
- Volume
- Surface Area
- Relationship between Volume and Surface Area
- Comparisons with Ratios
- Fractions
- Decimals and Percents
- Multiplying and Dividing Fractions
Be Prepared to
- give implicit directions on what they are to do. For example, "Today we are going to record datain the table on the worksheet and see if we can find a formula ..."
- answer the question "What does it mean by the n-th case?"
- discuss infinity, length, finding patterns in numbers, ect.