Koch's Snowflake

What is Koch's Snowflake?

This activity allows the user to step through the generation of a fractal made from deforming a line by bending it.

The Koch Curve was studied by Helge von Koch in 1904. When considered in its snowflake form, (see below) the curve is infinitely long but surrounds finite area.

To build the original Koch curve, start with a line segment 1 unit long. (Iteration 0, or the initiator)

Replace each line segment with the following generator:

Note that we are really taking the original line segment and replacing it with four new segments, each 1/3 the length of the original. Repeat this process on all line segments. Stages 0, 1, and 2 are shown below.

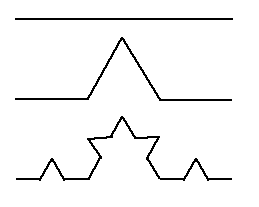
The limit curve of this process is the Koch curve. It has infinite length. Notice also that another feature that results from the iterative process is that of self-similarity, i.e., if we magnify or "zoom in on" part of the Koch curve, we see copies of itself.

The idea of the Koch curve was extended to the Koch "Snowflake" by applying the same generator to all three sides of an equilateral triangle; below are the first 4 iterations.

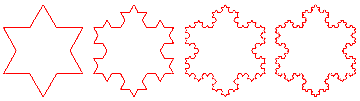
In the limit, the snowflake has infinite perimeter and finite area.

Related Resources

• Activity Another Hilbert Curve Generator
• Activity Hilbert Curve Generator
• Activity Recursion
• Discussion about Recursion
• Discussion about Self-Similarity
• Worksheet Emerging Patterns Worksheet
• Worksheet Emerging Patterns Worksheet (doc)
• Worksheet Koch's Snowflake Exploration Questions
• Worksheet Koch's Snowflake Exploration Questions (doc)

How Do I Use This Activity?

This activity allows the user to step through the generation of a fractal made from deforming a line by bending it.

Controls and Output

• The Next Stage and Previous Stage buttons at the bottom of the applet control which stage of the fractal that is being viewed.
• The Output Box at the top of the applet lists the current stage's number of individual line segments and the individual segment length.

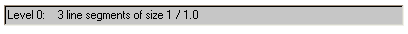
Description

This activity allows the user to step through the process of building the Koch Snowflake. This activity would work well in groups of two to four for about thirty to thirty-five minutes if you use the exploration questions and five minutes otherwise.

Place in Mathematics Curriculum

This activity can be used to:

• practice students' fraction manipulation skills
• practice students' pattern finding skills
• practice students' area and perimeter skills
• demonstrate the complexity of infinity
• motivate the ideas of self-similarity and recursion
• demonstrate fractal objects
• motivate the idea of a limit

Be Prepared to

• give implicit directions on what they are to do. For example, "Today we are going to record datain the table on the worksheet and see if we can find patterns in the numbers ..."
• answer the question "What does it mean by the n-th case?"
• discuss infinity, length, finding patterns in numbers, etc.

Related Resources

• Activity Another Hilbert Curve Generator
• Activity Hilbert Curve Generator
• Activity Recursion
• Discussion about Recursion
• Discussion about Self-Similarity
• Lesson on Emerging Patterns
• Lesson on Introduction to Fractals: Infinity, Self-Similarity and Recursion
• Lesson on Patterns in Fractals
• Worksheet Emerging Patterns Worksheet
• Worksheet Emerging Patterns Worksheet (doc)
• Worksheet Koch's Snowflake Exploration Questions
• Worksheet Koch's Snowflake Exploration Questions (doc)