Julia Sets

What is Julia Sets?

This activity allows the user to investigate the Julia sets associated with functions f(Z) = Z^2 + C for any complex number C=(a,b) in the circle of radius 2.

To understand Julia sets and ultimately the Mandelbrot set -- the world's most famous fractal -- we need to be able to find the boundary between the prisoner and escapee sets for a particular C.

An example of a function is: f(Z) = Z^2 + (.5,.5). If we start with the point (0,0) and plug it into the function:

f(0,0) = (0,0)^2 + (.5,.5) = (0,0) + (.5,.5) = (.5,.5)
f(.5,.5) = (.5,.5)^2 + (.5,.5) = (0,.5) + (.5,.5) = (.5,1)
f(.5,1) = (.5,1)^2 + (.5,.5) = (-.75,1) + (.5,.5) = (-.25,1.5)
f(-.25,1.5) = (-.25,1.5)^2 + (.5,.5) = (-2.1875,-.75) + (.5,.5) = (-1.6875,-.25)
f(-1.6875,-.25) = (-1.6875,-.25)^2 + (.5,.5) = (2.7852,.84375) + (.5,.5) = (3.2852,1.34375)

Here is a picture:

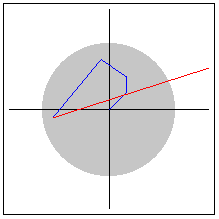
This is in the escapee set for C=(.5,.5). If we continue this process for lots of points we can get a feel for the picture of the Julia set. For C=(.5,.5) we get:

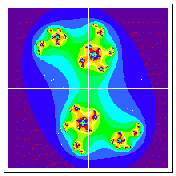
Notice that there are no black areas on this image. (Black would denote the prisoners.) There are prisoners, but they are completely scattered around and isolated from each other. This forces the Julia set -- the points that neither are prisoners or escapees -- to be completely disconnected from each other. The other colors on the picture are the escapees, and the different colors denote how quickly the point's orbit jumped out of the circle of radius 2.

Here's another one with an obvious prisoner set; C = (0,0).

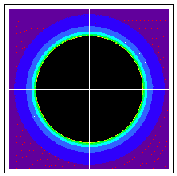
This has a nice big connected set of prisoners -- giving a connected Julia set, the circle of radius 1. Mandelbrot found that these are the only two things that happen, either the Julia set is fractal dust (totally disconnected) or it is one piece.

Here are a few of the more popular Julia sets:

C = (-1,0):

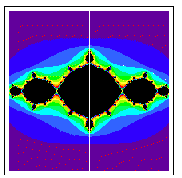
C = (-.1,.8):

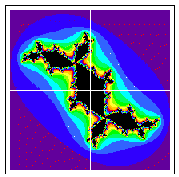
C = (.5,0):

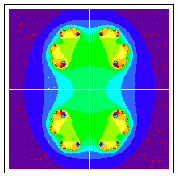
C = (-.8,.4):

The first two are connected and the last two are fractal dust. This is the basis for the Mandelbrot set.

Related Resources

• Activity The Mandelbrot Set
• Activity Two Variable Function Pump
• Discussion about Introduction to the Coordinate Plane and Coordinates
• Discussion about Prisoners and Escapees--Julia Sets
• Discussion about The Mandelbrot Set
• Discussion about Two Variable Functions
• Worksheet Julia Set Exploration Questions
• Worksheet Julia Set Exploration Questions (doc)

How Do I Use This Activity?

This activity allows the user to investigate the Julia sets associated with functions f(Z) = Z^2 + C for any complex number C=(a,b) in the circle of radius 2.

Controls and Output

• The rectangular area at the top of the screen is where the Julia set is drawn. Black points are prisoners; colored points are escapees (color differences indicate how quickly they escape from the circle of radius 2).
• The Constant text box at the bottom is for the value of C for which you are interested in viewing the Julia set. To change the C value, either click the up/down arrows or enter a number directly in the text field. For best results, keep the C value under 2.
  
• Press the Draw button to clear the current Julia Set and draw a new one with the entered values for the constant. Since the Set is redrawn with each press of an up/down arrow, the only time this button will make a change to the graph is when numbers have been directly entered into the text fields (without the pressing of the arrow buttons).
  
• The Change Step Size button changes the amount by which the C value increases each time you click the up or down arrow.
  

Description

This activity allows the user to investigate the Julia sets associated with functions f(Z) = Z^2 + C for any complex number C=(a,b) in the circle of radius 2. This activity would work well in groups of two to four for about twenty-five minutes if you use the exploration questions and ten minutes otherwise.

Place in Mathematics Curriculum

This activity can be used to:

• practice students' arithmetic skills
• practice students' point plotting skills
• introduce students to complex numbers
• investigate the notions of Julia sets, prisoners and escapees
• motivate the Mandelbrot set

Be Prepared to

• give implicit directions on what they are to do. For example "Today we are going to find out about prisoners, escapees, and complex numbers by using the Julia set activity as well as the Two Variable Function Pump and the Julia set worksheet..."
• answer the question "What is a prisoner and what is an escapees?"
• discuss complex numbers, and how to plot points

Related Resources

• Activity The Mandelbrot Set
• Activity Two Variable Function Pump
• Discussion about Introduction to the Coordinate Plane and Coordinates
• Discussion about Prisoners and Escapees--Julia Sets
• Discussion about The Mandelbrot Set
• Discussion about Two Variable Functions
• Lesson on Introduction to Functions
• Lesson on The Mandelbrot Set
• Worksheet Julia Set Exploration Questions
• Worksheet Julia Set Exploration Questions (doc)