What is The Mandelbrot Set?
This activity allows the user to investigate the Mandelbrot set associated with functions
f(Z) = Z^2 + C.
To understand the Mandelbrot set -- the world's most famous fractal -- we need to use the fact that Julia sets for a particular C in the function above are either fractal dust or are one connected piece.
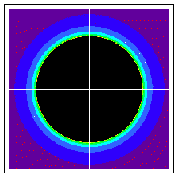
For C=(.5,.5) we get the fractal dust Julia set:
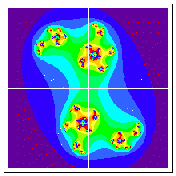
Here's one with connected Julia set; C = (0,0).
Mandelbrot came up with the idea of plotting the Cs with connected Julia sets, and found that the boundary was very interesting -- and Fractal!
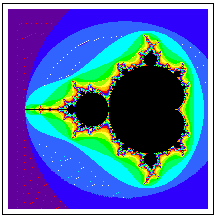
The black points are the Cs with connected Julia sets, and the colored points are Cs with fractal dust Julia sets. Mandelbrot proved that a person could tell if the Julia set would be fractal dust or not depending on whether the starting point (0,0) was a prisoner (connected) or escapee (dust). So the colors come from how quickly the starting point (0,0) orbit gets out of the circle of radius 2.
How Do I Use This Activity?
This activity allows the user to investigate the Mandelbrot set associated with the functions
f(Z) = Z^2 + C
Controls and Output
-
The rectangular area at the top of the screen is where the Mandelbrot or Julia Set is
drawn. To
zoom in on part of the Mandelbrot Set or Julia set, click in one corner of the area that you want
to zoom in on. Holding down the mouse button, move the mouse to the diagonally opposite
corner of the region you want to zoom in on. The region that you have selected will change
colors as you move the mouse. When you have selected the zoom region, release the mouse
button and the screen will be redrawn.
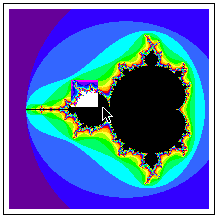
-
If you are looking at the Mandelbrot Set and want to see the Julia Set, click on the
checkbox that says
Show Julia Set on click. Then click on the Mandelbrot set. The Julia Set corresponding to the point you clicked
will be shown.

-
If you are looking at the Julia Set and want to see the Mandelbrot Set, click on the
checkbox that says
Show Mandelbrot Set on click. Then click on the Julia Set to see the Mandelbrot Set again.

-
To start over, just click the large, friendly button labeled
Start Over. You will see the same screen that you saw when you started the applet.

Description
This activity allows the user to investigate the Mandelbrot set associated with functions.
f(Z) = Z^2 + C
This activity would work well in mixed ability groups of two or three for about thirty minutes
if you use the
exploration questions and ten minutes otherwise.
Place in Mathematics Curriculum
This activity can be used to:
- practice students' arithmetic skills
- practice students' point plotting skills
- introduce students to complex numbers
- investigate the notions of Julia sets, prisoners and escapees
- explore the Mandelbrot set
Standards Addressed
Grade 6
-
Geometry
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
Grade 7
-
Geometry
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
Grade 8
-
Geometry
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
Grade 9
-
Geometry
- The student demonstrates an understanding of geometric relationships.
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
- The student demonstrates a conceptual understanding of geometric drawings or constructions.
Grade 10
-
Geometry
- The student demonstrates an understanding of geometric relationships.
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
- The student demonstrates a conceptual understanding of geometric drawings or constructions.
Number and Quantity
-
The Complex Number System
- Represent complex numbers and their operations on the complex plane.
Grades 9-12
-
Algebra
- Understand patterns, relations, and functions
-
Geometry
- Specify locations and describe spatial relationships using coordinate geometry and other representational systems
- Use visualization, spatial reasoning, and geometric modeling to solve problems
-
Measurement
- Apply appropriate techniques, tools, and formulas to determine measurements
Geometry
-
Geometry and Measurement
- Competency Goal 2: The learner will use geometric and algebraic properties of figures to solve problems and write proofs.
Algebra II
-
Algebra
- Competency Goal 2: The learner will use relations and functions to solve problems.
-
Numbers and Operations
- Competency Goal 1: The learner will perform operations with complex numbers, matrices, and polynomials.
Technical Mathematics I
-
Geometry and Measurement
- Competency Goal 2: The learner will measure and apply geometric concepts to solve problems.
Technical Mathematics II
-
Geometry and Measurement
- Competency Goal 1: The learner will use properties of geometric figures to solve problems.
Advanced Functions and Modeling
-
Algebra
- Competency Goal 2: The learner will use functions to solve problems.
Discrete Mathematics
-
Algebra
- Competency Goal 3: The learner will describe and use recursively-defined relationships to solve problems.
Integrated Mathematics III
-
Algebra
- Competency Goal 3: The learner will use relations and functions to solve problems.
-
Geometry and Measurement
- Competency Goal 2: The learner will use properties of geometric figures to solve problems.
Integrated Mathematics IV
-
Algebra
- Competency Goal 4: The learner will use relations and functions to solve problems.
-
Number and Operations
- Competency Goal 1: The learner will operate with complex numbers and vectors to solve problems.
Be Prepared to
- give implicit directions on what they are to do. For example "Today we are going to look at the Mandelbrot set and see what we can learn about it. We will try to answer the questions on the worksheet..."
- answer the question "What are we supposed to get from this?"
- discuss how the Mandelbrot set is made