Two Variable Function Pump

What is Two Variable Function Pump?

This activity allows the user to step through plotting a two-variable function, and to judge whether a given starting point is a prisoner or an escapee, in order to understand complex numbers and Julia sets.

To understand Julia sets and ultimately the Mandelbrot set -- the world's most famous fractal -- we need to be able to calculate with and plot quadratic functions of complex numbers. The easiest way to think of complex numbers is as an ordered pair of numbers. Functions of these numbers can be described as "input-output machines" as usual, only this time an ordered pair goes in and an ordered pair comes out.

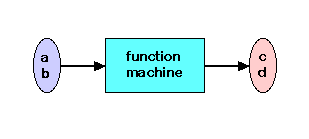
Basic Operations are revised for this new situation as:

An example of a function is:

        f(Z) = Z^2 + (0.5,0.5)
      

        f(0,0)  = (0,0)^2 + (0.5,0.5) = (0,0) + (0.5,0.5)= (0.5,0.5)

 	f(0.5,0.5) = (0.5,0.5)^2 + (0.5,0.5) = (0,0.5) + (0.5,0.5) = (0.5,1)

 	f(0.5,1) = (0.5,1)^2 + (0.5,0.5) = (-0.75,1) + (0.5,0.5) = (-0.25,1.5)

 	f(-0.25,1.5) = (-0.25,1.5)^2 + (0.5,0.5) = (-2.1875,-0.75) + (0.5,0.5) = (-1.6875,-0.25)

 	f(-1.6875,-0.25) = (-1.6875,-0.25)^2 + (0.5,0.5) = (2.7852,0.84375) + (0.5,0.5) = (3.2852,1.34375)
      

Here is a picture:

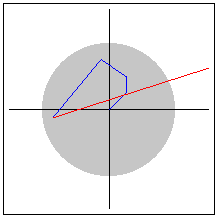
Here the points seem to be jumping around, getting farther away from (0,0) and finally leaving the gray circle of radius 2. We can try other starting points and look at what happens in each situation. There are three things that can happen. The points can:

• Get closer and closer to 0 -- we say they approach 0. These are the prisoners.
• Get larger and larger -- we say they approach infinity. These are the escapees. We know that they are escapees if they are further away from the origin than 2 units.
• Get trapped -- these points are the boundary points between the prisoners and escapees. The set of all of these points for a function is called the Julia Set.

Julia sets are the main building blocks for the Mandelbrot set. We find the Julia sets by looking for the boundary between prisoners and escapees.

Related Resources

• Activity Algebra Four
• Activity Algebra Quiz
• Activity Julia Sets
• Activity The Mandelbrot Set
• Discussion about Introduction to the Coordinate Plane and Coordinates
• Discussion about Prisoners and Escapees--Julia Sets
• Discussion about The Mandelbrot Set
• Worksheet Two-Variable Function Pump Exploration Questions
• Worksheet Two-Variable Function Pump Exploration Questions (doc)

How Do I Use This Activity?

This activity allows the user to step through plotting a two-variable function, and to judge whether a given starting point is a prisoner or an escapee, in order to understand complex numbers and Julia sets.

Controls and Output

• The boxes near the bottom of the applet are where you enter a Starting Point and a Constant, C, for the quadratic function

              f(Z) = Z^2 + C
            

  , that you want to iterate.
• Whenever you change the Starting Point or Constant, press the Restart button to start a fresh graph with those values. Press the Next Step button to calculate the next iteration.

• The Graph shows the path (also called the orbit) of the starting point as it is plugged into the function. The red line is the path from the previous point to the most recent one. If the orbit path goes outside the gray circle of radius 2, the starting point is guaranteed to be an escapee.

  

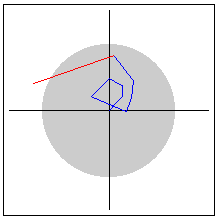
  The List on the left is another way to look at the values of the function -- as ordered pairs.

Description

This activity allows the user to step through plotting a two-variable function, and to judge whether a given starting point is a prisoner or an escapee, in order to understand complex numbers and Julia sets.

This activity would work well in mixed ability groups of three to five for about forty minutes if you use the exploration questions and twenty minutes otherwise.

Place in Mathematics Curriculum

This activity can be used to:

• practice students' arithmetic skills
• practice students' point plotting skills
• introduce students to complex numbers
• motivate the notions of Julia sets, prisoners and escapees

Be Prepared to

• give implicit directions on what they are to do. For example "Today we are going to find out about prisoners, escapees, and complex numbers by using the Two-Variable Function Pump activity and it's worksheet..."
• answer the question "What is a prisoner and what is an escapee?"
• discuss complex numbers, and how to plot points

Related Resources

• Activity Algebra Four
• Activity Algebra Quiz
• Activity Julia Sets
• Activity The Mandelbrot Set
• Discussion about Introduction to the Coordinate Plane and Coordinates
• Discussion about Prisoners and Escapees--Julia Sets
• Discussion about The Mandelbrot Set
• Lesson on Cartesian Coordinate System
• Lesson on Introduction to Functions
• Lesson on The Mandelbrot Set
• Worksheet Two-Variable Function Pump Exploration Questions
• Worksheet Two-Variable Function Pump Exploration Questions (doc)