Regression

What is Regression?

Correlation and regression are used regularly in statistical analysis. Correlation is used to see if a relationship exists between two variables and can be used to answer questions like these: Do you think there is any relationship between:

• the amount of time you spend studying for a test and the grade you make?
• the amount of time a team spends practicing and the number of wins they have in a season?
• how tall you are and your weight?
• the type f shoes you wear and how fast you can run?

If a relationship is found then correlation can be used to determine how strong the relationship is. Once a correlation has been discovered, regression is used to find the equation used to relate the two variables. This equation can tell you if the two variables are positively or negatively related.

Related Resources

• Activity Multiple Linear Regression
• Activity Scatter Plot
• Discussion about Bivariate Data Relations
• Discussion about Correlation Coefficients
• Discussion about Finding Residuals
• Discussion about Graphing and Interpreting Bivariate Data
• Discussion about Independent and Dependent Variables
• Discussion about Line of Best Fit
• Discussion about Outliers
• Discussion about Univariate Data and Bivariate Data
• Discussion about Using Residuals to Identify a Line of Good Fit
• Worksheet Regression Exploration Questions
• Worksheet Regression Exploration Questions (doc)

How Do I Use This Activity?

The regression applet is designed to allow the user to plot a bivariate data set, determine the line of best fit for their data, and then check the accuracy of their line of best fit.

Controls and Output

• First, the user needs to input their data. This can be done one of two ways.
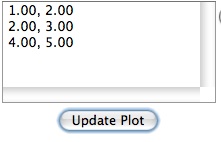
  1. The user can type the coordinates in the data box and click the Update Plot button. If you have trouble copying data from the applet and pasting it into an Excel spreadsheet, please see our Excel Copy/Paste Help.
     
     
  2. The user can plot points on the grid by selecting the Add Points button then placing the mouse over the desired location on the grid, clicking, and repeating this process for each data point.
• When the user has finished entering the data, they can try to create a line of best fit by checking the Fit your own line box.
• A green line will appear on the grid once the Fit your own line box has been checked. The user can move this by checking the Move Fit Line button then clicking on the green circles and dragging them to the desired location.
• The user can check the accuracy of their line of best fit by checking the Display line of best fit box.
• r is the linear correlation coefficient. r describes the strength of the linear relationship. r is a number between -1 and 1. If r = 0 there is no correlation between the data. If the r is positive, the data have a positive correlation. If the r is negative, the data have a negative correlation. The closer the r is to 1, the stronger the positive correlation. The closer the r is to -1, the stronger the negative correlation.
• Y denotes the line equation.
• The user can remove points by either deleting them from the data box and clicking the Update Plot button or by checking the Remove Points box and then clicking on the unwanted points on the grid.
• The user can move points by checking the Move Points box, then clicking on, and dragging the point they wish to move to the desired new location.
• Zoom/Pan buttons. In the upper right corner of the graph, there are three buttons with pictures of magnifying glasses. From top to bottom these buttons represent zoom in, zoom out, and pan, respectively.
  • To zoom in, click the top button to depress, then click and drag over the area of the graph for which you wish to zoom to. The images below show the preimage as the user drags over the area in which to zoom and the resulting zoomed image. Note that after clicking and dragging over the selected area, the zoom in button is automatically released.
  • To zoom out, simply click the middle button. The graph will automatically zoom out by doubling the min and max values of the axes.
  • To use the pan feature, click the bottom magnifying glass button to depress it. Click and drag over the graph and the graph will pan around according to the movement of the mouse. Upon releasing the mouse, the pan button is released.
  • The user can show the residuals by clicking the Show Residuals button.
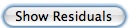
  • Once the user clicks the Show Residuals button a residuals screen appears. In the first column of the table located at the top of the residuals screen are the x-coordinates of each data point. In the second column are the residuals from your line. And in the third column are the residuals from the line of best fit. Located at the bottom of the residuals screen is a Residuals Plot. If the Display line of best fit box is checked, red dots will appear on the graph. If the Fit your own line box is checked, green dots will appear on the graph. If both the Display line of best fit and Fit your own line are checked, both red and green dots will appear on the graph. This graph depicts the distance between the lines of best fit and the actual data points.
  • The user can reset the graph to its original state by clicking the reset button located at the bottom right side of the screen.