What is Transmographer 2?
This applet is an expanded version of TransmoGrapher. It allows the user to explore the world of translations, reflections, and rotations. It allows the user to translate polygons on both the x and y-axes. The user can also reflect the figure across any line and rotate it around any point in the plane.
How Do I Use This Activity?
This applet allows the user to explore the world of transformations, reflections, and rotations. It allows the user to transform polygons with up to 12 user defined vertices on the coordinate plane.
Controls and Output
-
General Information:
- Each vertex of the polygon is colored a different color to help you see the orientation of the polygon. Whenever you perform a translation, reflection, or rotation the polygon is redrawn in its new position and orientation, and a "ghost" polygon is drawn in gray in the previous position. This will help you remember where the polygon was before the transformation.
-
Creating a New Polygon:
-
To create a new polygon, use the panel next to the coordinate plane titled "New
Polygon." Enter the number of vertices (between 3 and 12) you want the new polygon to
have in the box labeled "How many vertices?" and click the Go! button.

-
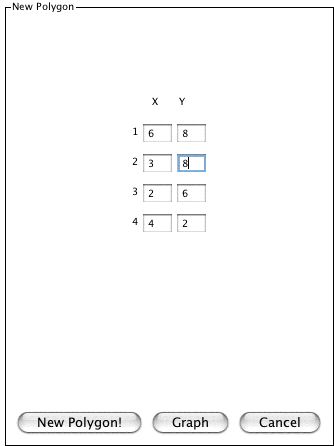
You will then see a new panel containing two columns of text boxes: one for x
coordinates and one for y coordinates.
-
Enter the coordinates of each vertex. All coordinates must be integers. When you are
done, preview the shape in the coordinate plane by clicking on the
 button. If you want to change the number of vertices, click on the
button. If you want to change the number of vertices, click on the
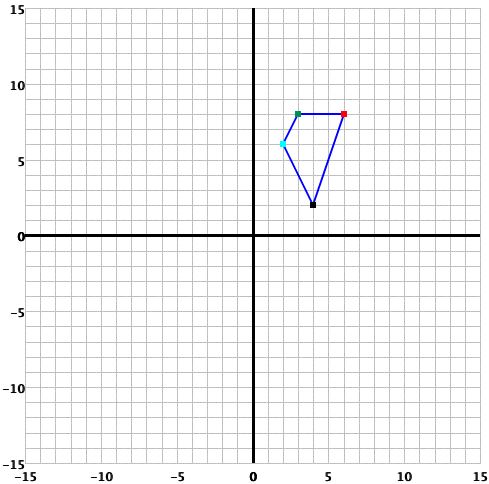
 button. This new polygon will be drawn on the coordinate plane:
button. This new polygon will be drawn on the coordinate plane:
-
If you are not satisfied with this shape and wish to return to the orginal shape,
press the Cancel button.

-
To create a new polygon, use the panel next to the coordinate plane titled "New
Polygon." Enter the number of vertices (between 3 and 12) you want the new polygon to
have in the box labeled "How many vertices?" and click the Go! button.
-
Translate Controls:
-
In the appropriate spaces, type the number of units you want to translate the shape on
the X-axis and on the Y-axis. The panel is under the coordinate plane and it looks
like:

-
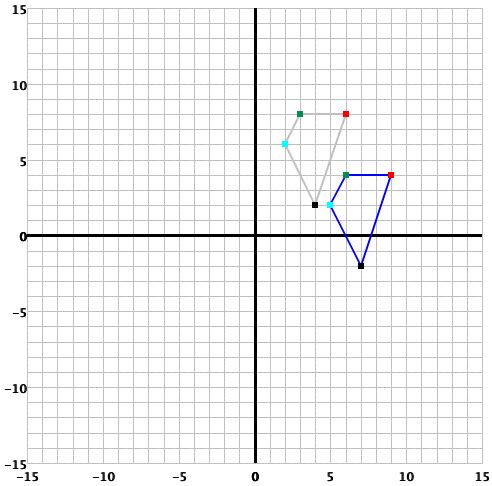
Both of these numbers must be integers. Then click the
 button to translate the polygon. The translation will appear on the coordinate plane
like:
button to translate the polygon. The translation will appear on the coordinate plane
like:
-
In the appropriate spaces, type the number of units you want to translate the shape on
the X-axis and on the Y-axis. The panel is under the coordinate plane and it looks
like:
-
Reflect Controls:
-
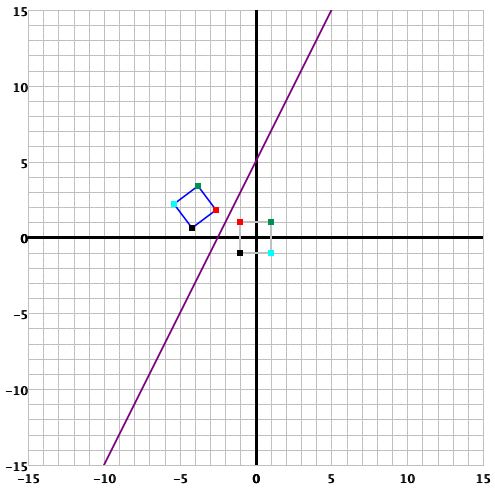
To reflect across a non-vertical line, click the circle beside the words "across y = "
and then enter the slope and y-intercept of the line you want to reflect across (both
of these numbers must be integers). This is located below the coordinate plane. For
instance, the following example will cause a reflection across y = 2x + 5 when you
click the
 button:
button:

-
The graph of this reflection is:
-
To reflect across a vertical line, click the circle beside the words "across x = " and
enter the x-coordinate of the line you want to reflect across (this number must be an
integer). Again, this is located under the coordinate plane. For instance, the
following example will cause a reflection across x = 3 when you click the
 button:
button:

-
The graph of this reflection is:
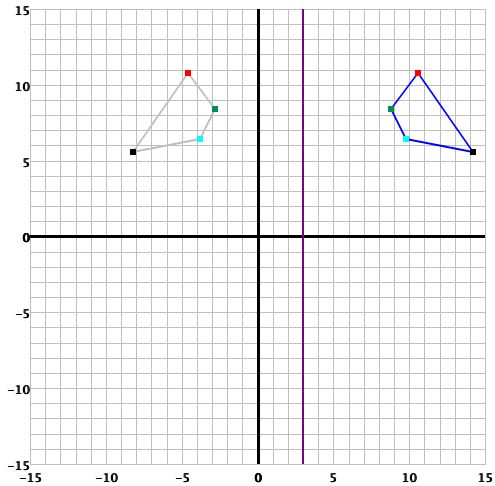
-
To reflect across a non-vertical line, click the circle beside the words "across y = "
and then enter the slope and y-intercept of the line you want to reflect across (both
of these numbers must be integers). This is located below the coordinate plane. For
instance, the following example will cause a reflection across y = 2x + 5 when you
click the
-
Rotate Controls:
-
Enter the number of degrees (an integer) for a rotation of the polygon in the
appropriate box. Then, below that, enter the coordinates of the center of rotation.
The x and y values must be integers. Then click the button
 to do the rotation. The panel looks like:
to do the rotation. The panel looks like:

-
The graph of this rotation is:
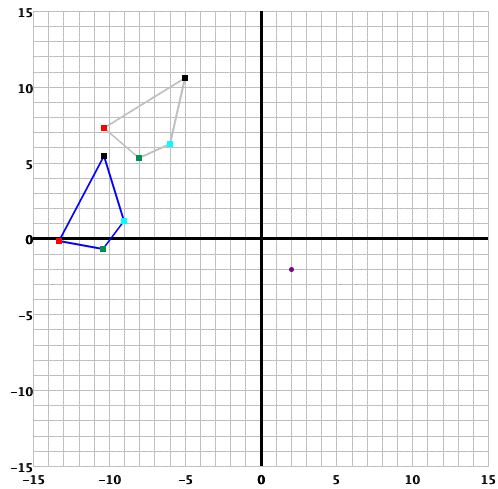
-
Enter the number of degrees (an integer) for a rotation of the polygon in the
appropriate box. Then, below that, enter the coordinates of the center of rotation.
The x and y values must be integers. Then click the button
Description
This activity allows the user to experiment with translation, reflection and rotation in the Cartesian coordinate plane. This activity would work well in mixed ability groups of two or four for about forty-five minutes if you use the exploration questions or the worksheet and fifteen to twenty minutes otherwise. If you wish to use both supplements, this activity will take approximately sixty minutes.
Place in Mathematics Curriculum
This activity can be used to:
- illustrate plotting basic shapes on the Cartesian coordinate system
- develop students mental visualization skills
- introduce the ideas of translation, reflection and rotation
- practice students skills at translation, reflection and rotation
Standards Addressed
Grade 3
-
Geometry
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
- The student demonstrates understanding of position and direction.
- The student demonstrates a conceptual understanding of geometric drawings or constructions.
Grade 4
-
Geometry
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
- The student demonstrates understanding of position and direction.
- The student demonstrates a conceptual understanding of geometric drawings or constructions.
Grade 5
-
Geometry
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
- The student demonstrates understanding of position and direction.
- The student demonstrates a conceptual understanding of geometric drawings or constructions.
Grade 6
-
Geometry
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
- The student solves problems (including real-world situations) using perimeter, area, or volume.
- The student demonstrates understanding of position and direction.
Grade 7
-
Geometry
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
- The student solves problems (including real-world situations).
- The student demonstrates understanding of position and direction.
Grade 8
-
Geometry
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
- The student solves problems (including real-world situations).
- The student demonstrates understanding of position and direction.
Grade 9
-
Geometry
- The student demonstrates an understanding of geometric relationships.
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
- The student demonstrates understanding of position and direction when solving problems (including real-world situations).
- The student demonstrates a conceptual understanding of geometric drawings or constructions.
Grade 10
-
Geometry
- The student demonstrates an understanding of geometric relationships.
- The student demonstrates conceptual understanding of similarity, congruence, symmetry, or transformations of shapes.
- The student demonstrates understanding of position and direction when solving problems (including real-world situations).
- The student demonstrates a conceptual understanding of geometric drawings or constructions.
Eighth Grade
-
Geometry
- Understand congruence and similarity using physical models, trans- parencies, or geometry software.
Geometry
-
Congruence
- Experiment with transformations in the plane
- Understand congruence in terms of rigid motions
Grades 3-5
-
Geometry
- Apply transformations and use symmetry to analyze mathematical situations
Grade 6
-
Number and Operations, Measurement, Geometry, Data Analysis and Probability, Algebra
- COMPETENCY GOAL 3: The learner will understand and use properties and relationships of geometric figures in the coordinate plane.
Technical Mathematics I
-
Algebra
- Competency Goal 3: The learner will describe the transformation of polygons in the coordinate plane algebraically.
5th Grade
-
Geometry
- The student will demonstrate through the mathematical processes an understanding of congruency, spatial relationships, and relationships among the properties of quadrilaterals.
4th Grade
-
Geometry
- Standard 4-4: The student will demonstrate through the mathematical processes an understanding of the relationship between two- and three-dimensional shapes, the use of transformations to determine congruency, and the representation of location and movement within the first quadrant of a coordinate system.
5th Grade
-
Geometry
- The student will develop an understanding of geometric concepts and relationships as the basis for geometric modeling and reasoning to solve problems involving one-, two-, and three-dimensional figures.
3rd Grade
-
Geometry
- Content Standard 3.0 The student will develop an understanding of geometric concepts and relationships as the basis for geometric modeling and reasoning to solve problems involving one-, two-, and three-dimensional figures.
4th Grade
-
Geometry
- The student will develop an understanding of geometric concepts and relationships as the basis for geometric modeling and reasoning to solve problems involving one-, two-, and three-dimensional figures.
Grade 4
-
Geometry and Spatial Reasoning
- 9. The student connects transformations to congruence and symmetry.
Grade 5
-
Geometry and Spatial Reasoning
- 8. The student models transformations.
Grade 8
-
Geometry and Spatial Reasoning
- 6. The student uses transformational geometry to develop spatial sense.
4th Grade
-
Geometry
- 4.17.c The student will investigate congruence of plane figures after geometric transformations such as reflection (flip), translation (slide) and rotation (turn), using mirrors, paper folding, and tracing.
5th Grade
-
Geometry
- 5.15e The student, using two-dimensional (plane) figures (square, rectangle, triangle, parallelogram, rhombus, kite, and trapezoid) will recognize the images of figures resulting from geometric transformations such as translation (slide), reflection (flip), or rotation (turn).
Textbooks Aligned
Grade Eight
-
Kaleidoscopes, Hubcaps, and Mirrors
- Investigation One: Three Types of Symmetry
- Investigation Two: Symmetry Transformations
- Investigation Three: Transforming Coordinates
- Investigation Four: Symmetry and Algebra
Book 1
-
Module 2 - Patterns and Designs
- Section 4: Translations, Rotations, Reflections
Book 2
-
Module 4 - The Art of Motion
- Section 3: Rotations and Symmetry, Reflections and Symmetry
- Section 5: Translations
- Section 5: Solving 2-Step Equations
6th
-
Module 8 - MATH-Thematical Mix
- Section 5: Transformations
7th
-
Module 4 - The Art of Motion
- Section 4: Rotations and Reflections
- Section 6: Translations, Similarity, and Two-Step Equations
8th
-
Module 6 - Visualizing Change
- Section 4: Algorithms and Transformations
Book 1
-
Designing Spaces
- Lesson 2: Seeing Around the Corners
Book 2
-
Getting In Shape
- Lesson 4: Tiling with Triangles
Grade 5
-
Figuring All the Angles
- Measuring Angles
- Rectangular Coordinates
Grade 7
-
Triangles and Beyond
- Parallel Lines
- Transformations
Be Prepared to
- define translation, reflection, and rotation and show examples
- explain net translation and net rotation