Crazy Choices Game

What is Crazy Choices Game?

This activity allows the user to run up to three different games of chance at once, allowing for comparison of experimental and theoretical probabilities.

Probability began in the middle of the seventeenth century by a man named Pascal. One day a man proposed a question about gambling. His question was "If I play a game that I have eight rolls to roll a six and I fail the first three times, how much of my bet should I get back?" The game involved chance just as most of games do now, such as Monopoly and card games. Las Vegas is a city that is dominated by people that have invested in this field of mathematics. Today, probability has found its way into the fields of science, medicine, and statistics.

This applet allows the user to experiment with multiple event probability by manipulating chance. It also introduces theoretical and experimental probability. As the user changes the number of trials they will see how much this affects the experimental probability. Theoretical probability is the outcome you would predict. The experimental probability is the actual outcome after running a given number of trials.

How Do I Use This Activity?

This activity allows the user to run up to three different games of chance at once, allowing for comparison of experimental and theoretical probabilities.

Controls and Output

  • This applet lets you simulate playing up to three games of chance at once. The games are organized into three columns. You do not have to input values for all three games every time. If you do not set the probabilities for a game, the applet will ignore that game when it runs.
  • Two items at the top of the applet let you describe each of three games that can be simulated. You can choose the type of game: throwing a die, picking cards from a deck, spinning a spinner, flipping a coin, or another game. In the text boxes below the type of game, describe what wins. For example, if the game is flipping a coin, what wins could be "heads." Note: these boxes have NOTHING to do with the actual calculation! They are for you to record your notes about what is being simulated. In the next section, you yourself have to enter the correct theoretical probabilities based on your analysis.
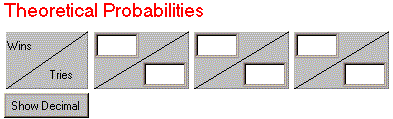
  • Under Theoretical Probabilities, you must enter the probability as a fraction of winning each game you have described. For instance, if the game was flipping a coin with heads winning, you would expect to win one time for every two tries. So you would enter "1" in the upper box (numerator) and "2" in the lower box (denominator). Clicking the Show Decimal button will show you the value you have typed in as a decimal.
  • To simulate playing the game, click the Run button. Beside the run button, you can set the number of times (up to 10,000) you want the game to be run. If the Add runs to total box is checked, these runs will be added to the previous totals. If it is unchecked, previous runs will be cleared.
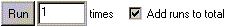
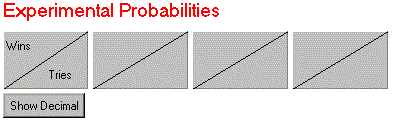
  • The results of playing the game are displayed in the Experimental Probabilities section.
  • The Clear Experimental Probabilities button erases all the data from previous runs of the game(s).

Description

This activity allows the user to run up to three different games of chance at once, allowing for comparison of experimental and theoretical probabilities. This activity would work well in groups of two for about twenty minutes if you use the exploration questions and ten minutes otherwise.

Place in Mathematics Curriculum

This activity can be used to:

  • introduce the notions of chance and probability
  • shows the difference between experimental and theoretical probability
  • motivate the notion of random numbers
  • motivate ideas from combinatorics

Standards Addressed

Grade 6

  • Statistics and Probability

    • The student demonstrates a conceptual understanding of probability and counting techniques.

Grade 7

  • Statistics and Probability

    • The student demonstrates a conceptual understanding of probability and counting techniques.

Grade 8

  • Statistics and Probability

    • The student demonstrates a conceptual understanding of probability and counting techniques.

Grade 9

  • Statistics and Probability

    • The student demonstrates a conceptual understanding of probability and counting techniques.

Grade 10

  • Statistics and Probability

    • The student demonstrates a conceptual understanding of probability and counting techniques.

Seventh Grade

  • Statistics and Probability

    • Investigate chance processes and develop, use, and evaluate probability models.

Statistics and Probability

  • Conditional Probability and the Rules of Probability

    • Understand independence and conditional probability and use them to interpret data
    • Use the rules of probability to compute probabilities of compound events in a uniform probability model

  • Making Inferences and Justifying Conclusions

    • Understand and evaluate random processes underlying statistical experiments
    • Make inferences and justify conclusions from sample surveys, experiments, and observational studies

  • Using Probability to Make Decisions

    • Calculate expected values and use them to solve problems
    • Use probability to evaluate outcomes of decisions

Grades 6-8

  • Data Analysis and Probability

    • Understand and apply basic concepts of probability

Grades 9-12

  • Data Analysis and Probability

    • Develop and evaluate inferences and predictions that are based on data
    • Formulate questions that can be addressed with data and collect, organize, and display relevant data to answer them
    • Understand and apply basic concepts of probability

Grade 6

  • Number and Operations, Measurement, Geometry, Data Analysis and Probability, Algebra

    • COMPETENCY GOAL 4: The learner will understand and determine probabilities.

Advanced Functions and Modeling

  • Data Analysis and Probability

    • Competency Goal 1: The learner will analyze data and apply probability concepts to solve problems.

Integrated Mathematics

  • Data Analysis and Probability

    • Competency Goal 3: The learner will analyze data and apply probability concepts to solve problems.

AP Statistics

  • Data Analysis and Probability

    • Competency Goal 3: The learner will collect and analyze data to solve problems.

  • Number and Operations

    • Competency Goal 1: The learner will analyze univariate data to solve problems.

6th Grade

  • Data Analysis and Probability

    • The student will demonstrate through the mathematical processes an understanding of the relationships within one population or sample.

7th Grade

  • Data Analysis and Probability

    • The student will demonstrate through the mathematical processes an understanding of the relationships between two populations or samples.

8th Grade

  • Data Analysis and Probability

    • The student will demonstrate through the mathematical processes an understanding of the relationships between two variables within one population or sample.

Grade 6

  • Probability and Statistics

    • 9. The student uses experimental and theoretical probability to make predictions.

Grade 8

  • Probability and Statistics

    • 11. The student applies concepts of theoretical and experimental probability to make predictions.

7th Grade

  • Probability and Statistics

    • 7.14 The student will investigate and describe the difference between the probability of an event found through simulation versus the theoretical probability of that same event.
    • 7.15 The student will identify and describe the number of possible arrangements of several objects, using a tree diagram or the Fundamental (Basic) Counting Principle.

4th Grade

  • Probability and Statistics

    • 4.19.b

5th Grade

  • Probability and Statistics

    • 5.17a The student will solve problems involving the probability of a single event by using tree diagrams or by constructing a sample space representing all possible results

8th Grade

  • Probability and Statistics

    • 8.11 The student will analyze problem situations, including games of chance, board games, or grading scales, and make predictions, using knowledge of probability.
    • 8.11 The student will analyze problem situations, including games of chance, board games, or

Be Prepared to

  • give implicit directions on what they are to do. For example, "Today we are going to learn thedifference between experimental and theoretical probabilities by ..."
  • answer the question "What difference does it make what type of game I choose or what wins? Itdoesn't make a difference anyway."
  • discuss the terms outcome, probability, theoretical probability, experimental probability, event,etc.