Dice Table

What is Dice Table?

This activity allows the user to calculate the probability of each number (2-12) appearing when two dice are rolled. They also get practice converting probabilities into fractions, decimals, and percentages. Each number outcome can have more than one possible combination to make that number. For example the outcome of six has the possible combinations of 5+1, 4+2, and 3+3. Another term used in probability is permutations. This word refers to the arrangement of the values, for example 4+2=6 and 2+4=6.

Probability began in the middle of the seventeenth century by a man named Pascal. One day a man proposed a question about gambling. His question was "If I play a game that I have eight rolls to roll a six and I fail the first three times, how much of my bet should I get back?" The game involved chance just as most of games do now, such as Monopoly and card games. Las Vegas is a city that is dominated by people that have invested in this field of mathematics. Today, probability has found its way into the fields of science, medicine and statistics.

Related Resources

• Activity Adjustable Spinner
• Activity Buffon's Needle
• Activity Generalized Monty Hall
• Activity Racing Game with Two Dice
• Discussion about Divisibility
• Discussion about Equally Likely (Fair) Choice
• Discussion about Random Number Generators
• Discussion about Tables and Combinatorics
• Worksheet Two Dice Table Exploration Questions
• Worksheet Two Dice Table Exploration Questions (doc)
• Worksheet Two Dice Table Game Suggestions
• Worksheet Two Dice Table Game Suggestions (doc)

How Do I Use This Activity?

This activity allows the user to calculate the probability of each number (2-12) appearing when two dice are rolled, as well as get practice converting probabilities into fractions, decimals, and percentages.

Controls and Output

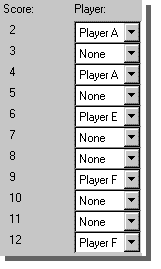
• To assign a winning sum (Score) to a player, select the player's name next to the score by clicking on the selection sign: next to that score, and then on the player's name; in the list that will appear. In our example, Player A wins if the score is 2 or 4, Player E wins if the sum is 6, and Player F wins if the sum is 9 or 12. Nobody wins if the dice produce the rest of the possible sums:
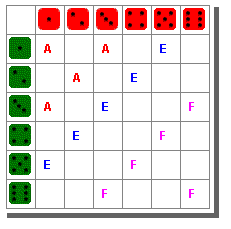
• The winning combinations of dice numbers for each player is shown in a table. For example, Player E (whose winning sum we set to be 6) wins for five different combinations of numbers on the green and red dice (Green 1 Red 5; Green 2 Red 4; Green 3 Red 3; Green 4 Red 2; and Green 5 Red 1):
• To study a particular player in detail, choose this player in the Select a player [____] menu by clicking on the selection sign: , and then on the player's name in the list that will appear. In our example, Player A is selected:
• To check the probability of winning for the selected player, use any of the four expressions of the probability, as follows.
• To check the probability by outcomes, type the numbers of outcomes for the player in the Q#1: The player wins in [____] out of [____] outcomes spaces. In our example, Player A wins in 4 out of 36 outcomes:
• Then click on the check #1 button to have the software verify your answer:x
• To check the probability by fractions, type the numerator and the denominator of the probability of the player winning in the Q#2: The probability to win as a simple fraction is [____] / [____] spaces. For Player A, the probability of winning is 1/9:
• Then click on the check #2 button to have the software verify your answer:
• To check the probability by decimals, type the probability of the player winning in the decimal form (rounded to four digits after the decimal point) in the Q#3: The same probability in decimal form rounded to four places is [____] space. For Player A, the probability of winning is .1111:
• Then click on the check #3 button to have the software verify your answer:
• To check the probability by percents, type the probability of the player winning in percents (rounded to two decimal places) in the Q#4: The same probability in percents rounded to two decimal places is [____] space. For Player A, the probability of winning is 11.11%:
• Then click on the check #4 button to have the software verify your answer:

Description

This activity allows the user to calculate the probability of each number (2-12) appearing when two dice are rolled. This activity would work well in same ability groups of two to four for about twenty to twenty-five minutes if you use the exploration questions and ten minutes otherwise.

Place in Mathematics Curriculum

This activity can be used to:

• practice students' fraction, decimal and percent manipulation skills
• introduce the notions of chance and probability
• motivate the notion of random numbers
• motivate ideas from combinatorics

Be Prepared to

• permit calculators or stop the whining about not having calculators quickly and permanently
• answer the question "How do I change a fraction to a decimal?"
• discuss ways to convert from fractions to decimal to percentages and back.

Related Resources

• Activity Adjustable Spinner
• Activity Buffon's Needle
• Activity Generalized Monty Hall
• Activity Racing Game with Two Dice
• Discussion about Divisibility
• Discussion about Equally Likely (Fair) Choice
• Discussion about Random Number Generators
• Discussion about Tables and Combinatorics
• Lesson on From Probability to Combinatorics and Number Theory
• Lesson on Ideas that Lead to Probability
• Lesson on Introduction to the Concept of Probability
• Lesson on Unexpected Answers
• Worksheet Two Dice Table Exploration Questions
• Worksheet Two Dice Table Exploration Questions (doc)
• Worksheet Two Dice Table Game Suggestions
• Worksheet Two Dice Table Game Suggestions (doc)