Positive Linear Function Machine

What is Positive Linear Function Machine?

This activity allows the user to explore simple linear functions; the function is determined by looking for patterns in the outputs. The functions available for exploration in the function machine activity have the following form:

          y = __ * x + __
        

The notion of a function is important in higher mathematics such as calculus and in areas which use mathematics such as physics. Any rule that assigns exactly one output to an input or list of inputs can be called a function.

Here are a few examples:

• Input the number of seconds after the starting gun in a race to get an output of the number of meters the runner has covered.

  Race Chart
  Number of Seconds (input)	1	4	7	8
  Meters covered (output)	5	20	35	40

• y = x - 6, where x is the place holder (also called a variable) for the input and y is the place holder for the output.

  Function y = x - 6
  X (input)	-3	0	7	8
  Y (output)	-9	-6	1	2

• The rule about only one output each time is crucial and must not be violated. For example, the table below cannot represent a function because 3 has two different outputs:

  Not a Function
  input	3	2	0	3
  output	4	-1	2	-3

• The functions produced by this machine are special because they all graph as straight lines. In fact, the slope of the line and the y-intercept of the line are easy to read from the formula:

          y = (slope) * x + (y-intercept)
        

• The slope tells us the rise over the run, and the intercept tells us where the line crosses the vertical axis when plotted:

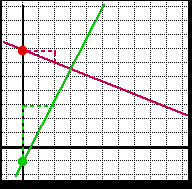
• Here the red line has intercept = 7 and slope = -1/2, and the green line has intercept = -1 and slope = 4/2.

Related Resources

• Activity Function Machine
• Activity Incline
• Activity Linear Function Machine
• Activity Number Cruncher
• Activity Whole Number Cruncher
• Discussion about Functions as Processes or Rules: "Function Machines"
• Discussion about Independent and Dependent Variables
• Discussion about Multi-Step Functions
• Discussion about Slope and Y-intercept
• Worksheet Four Quadrant Grid, 14x18
• Worksheet Four Quadrant Grid, 28x36
• Worksheet Linear Function Machine Game Explorations
• Worksheet Linear Function Machine Game Explorations (doc)

How Do I Use This Activity?

This activity allows the user to explore simple linear functions; the function is determined by looking for patterns in the outputs. The functions available for exploration in the function machine activity have the following form:

          y = __ * x + __
        

Object of the Game

A randomly selected "function machine" takes a number and produces another number according to a rule (a function). The goal of the game is to guess the rule. Possible rules in the game are: Y = N * X + K, where N and K are randomly selected whole numbers from 0 to 10.

Controls and Output

As an example, we use function Y = X + 2

• To find out what the machine will do with a number:
  • Type the number into the X= [____] space (in our example, number 5 is typed in):
    
  • Press the Enter button:
    
  • Observe the resulting number in the Y= [____] window (in our example, number 7 is the result):
    
  • You can input as many numbers as you need to find the rule
• To check if you guessed the rule right, type numbers in the Y = [___]*X + [___] spaces, and then press the Check formula button. You will see one of the two messages under the picture of the machine: either Correct answer! Try again!
• To set a new function machine (that is, a new rule), click once on the Set new function button:
  

• This activity will automatically record how successful you are at answering the questions. To view the score, press the Show Score button at the bottom of the activity and a pop-up window will appear with the scoreboard. To close this pop-up window press the Close button or click back on the main window.
• To pause the scoring, press the Active button at the bottom of the screen and it will change to a Paused button. To resume scoring, press the Paused button.
• To reset the scoreboard, open the scoreboard using the Show Score button and then press the Reset button.

Because this activity randomly generates questions, a feature called Seed Random has been implemented that allows multiple users using different computers to work on the same problem. See Seed Random Help for instructions on using this feature.

Description

This activity allows the user to explore simple linear functions; the function is determined by looking for patterns in the outputs. The function is always a simple line of the following form:

y = m*x + b

where m, the slope, and b, the y-intercept, can be any integer between 0 and 10. This activity would work well in same ability groups of two to three for about forty-five minutes if you use the exploration questions and ten to fifteen minutes otherwise.

Place in Mathematics Curriculum

This activity can be used to:

• practice students' pattern finding skills
• introduce basic notions from algebra
• motivate the idea of a function of one variable
• practice students' arithmetic skills

Be Prepared to

• answer the question "How do I figure out what the numbers are supposed to be? I don't know how to
• discuss pattern recognition, input, output, etc...

Related Resources

• Activity Function Machine
• Activity Incline
• Activity Linear Function Machine
• Activity Number Cruncher
• Activity Whole Number Cruncher
• Discussion about Functions as Processes or Rules: "Function Machines"
• Discussion about Independent and Dependent Variables
• Discussion about Multi-Step Functions
• Discussion about Slope and Y-intercept
• Lesson on Introduction to Functions
• Lesson on More Complicated Functions: Introduction to Linear Functions
• Worksheet Four Quadrant Grid, 14x18
• Worksheet Four Quadrant Grid, 28x36
• Worksheet Linear Function Machine Game Explorations
• Worksheet Linear Function Machine Game Explorations (doc)