What is Venn Diagrams?
Venn Diagrams were first developed by John Venn in the 1880s. They are useful for illustrating the relationships between sets. For example if we want to represent the set of all counting numbers, and illustrate how even numbers and multiples of 3 are related, we could draw the following picture:
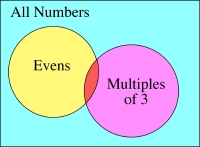
See how the circles overlap but not completely -- why? Because 6 is both even and a multiple of 3, but there are many numbers that are even and not multiples of 3 and vice versa. Numbers which are in both sets would be located in the little red sliver where the circles overlap.
How Do I Use This Activity?
This applet provides a series of Venn diagram questions. The user is given an object and must determine the region to which it belongs.
Controls and Output
-
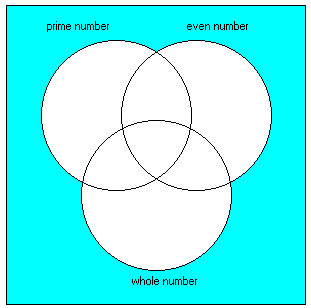
First, click in the specific region where the given number or object belongs. The area you
have chosen will be displayed in color. Below, the user has chosen the region where "prime
number" and "even number" overlap.

-
You may find an object or number that does not fit into any of the regions. You may select
the region outside the Venn diagram and the box around the diagram will be shown in color
to let you know that region is selected.
-
When you are confident that you have clicked on the right region, click
Check Answer to see if you are correct. If you have chosen the correct region, the program will tell
you so. If the correct region has not been chosen, the applet will respond with
"Incorrect". To see a new question, click
Next.

-
As you are answering questions within the applet you might decide you would like to up the
difficulty level or continue on 'All', which gives you a variety of all difficulty levels
from 1-3. Otherwise you can choose from level 1 which is easy, level 2 for medium, and
level 3 for hard.

-
This activity will automatically record how successful you are at answering the questions.
To view the score, press the
Show Score button at the bottom of the activity and a pop-up window will appear with the scoreboard.

- To close this pop-up window press the Close button or click back on the main window.
- To pause the scoring, press the Active button at the bottom of the screen and it will change to a Paused button. To resume scoring, press the Paused button.
- To reset the scoreboard, open the scoreboard using the Show Score button and then press the Reset button.
Description
This activity allows the user to explore Venn Diagrams and their various applications. This activity would work well in groups of two for about thirty to forty-five minutes if you use the exploration questions and fifteen to twenty minutes otherwise.
Place in Mathematics Curriculum
This activity can be used to:
- introduce the concept of Venn Diagrams.
- explore different types of Diagrams.
- apply Venn Diagrams as a tool for exploring various academic subjects
Standards Addressed
Grade 3
-
Process Skills
- The student demonstrates an ability to problem solve.
- The student communicates his or her mathematical thinking.
- The student demonstrates an ability to use logic and reason.
Grade 4
-
Process Skills
- The student demonstrates an ability to problem solve.
- The student communicates his or her mathematical thinking.
- The student demonstrates an ability to use logic and reason.
Grade 5
-
Functions and Relationships
- The student communicates his or her mathematical thinking.
- The student demonstrates an ability to use logic and reason.
-
Process Skills
- The student demonstrates an ability to problem solve.
- The student communicates his or her mathematical thinking.
- The student demonstrates an ability to use logic and reason.
Grade 6
-
Process Skills
- The student demonstrates an ability to problem solve.
- The student communicates his or her mathematical thinking.
- The student demonstrates an ability to use logic and reason.
-
Statistics and Probability
- The student demonstrates an ability to classify and organize data.
Grade 7
-
Process Skills
- The student demonstrates an ability to problem solve.
- The student communicates his or her mathematical thinking.
- The student demonstrates an ability to use logic and reason.
-
Statistics and Probability
- The student demonstrates an ability to classify and organize data.
Grade 8
-
Process Skills
- The student demonstrates an ability to problem solve.
- The student communicates his or her mathematical thinking.
- The student demonstrates an ability to use logic and reason.
-
Statistics and Probability
- The student demonstrates an ability to classify and organize data.
Grade 9
-
Process Skills
- The student demonstrates an ability to problem solve.
- The student communicates his or her mathematical thinking.
- The student demonstrates an ability to use logic and reason.
Grade 10
-
Process Skills
- The student demonstrates an ability to problem solve.
- The student communicates his or her mathematical thinking.
- The student demonstrates an ability to use logic and reason.
Fourth Grade
-
Operations and Algebraic Thinking
- Generate and analyze patterns.
Fifth Grade
-
Operations and Algebraic Thinking
- Analyze patterns and relationships.
Grades 6-8
-
Data Analysis and Probability
- Understand and apply basic concepts of probability
-
Geometry
- Use visualization, spatial reasoning, and geometric modeling to solve problems
Grade 3
-
Underlying Processes and Mathematical Tools
- 16. The student uses logical reasoning.
Grade 4
-
Underlying Processes and Mathematical Tools
- 16. The student uses logical reasoning.
Grade 5
-
Underlying Processes and Mathematical Tools
- 16. The student uses logical reasoning.
Be Prepared to
- explain all vocabulary words used in the applet.
- explain what happens when the object being classified does not fall under the categories of any of the circles
- give the categories for the class Venn diagram for question three in the exploration questions.