Triple Venn Diagram Shape Sorter

What is Triple Venn Diagram Shape Sorter?

Venn Diagrams were first developed by John Venn in the 1880's. They are useful for illustrating the relationships between sets. Each set is illustrated by a circle. When two circles overlap, this shows an intersection of the two sets. For more practice with one or two set Venn Diagrams, students may use the Venn Diagram Shape Sorter. When working with three sets, three circles are needed to illustrate all possible relationships among the sets. John Venn and other mathematicians have presented complicated diagrams for sets greater than three. Diagrams with one, two, or three circles are the most common. If we want to consider how the sets of positive integers, even integers, and multiples of 3 are related to one another, we could draw the following picture:

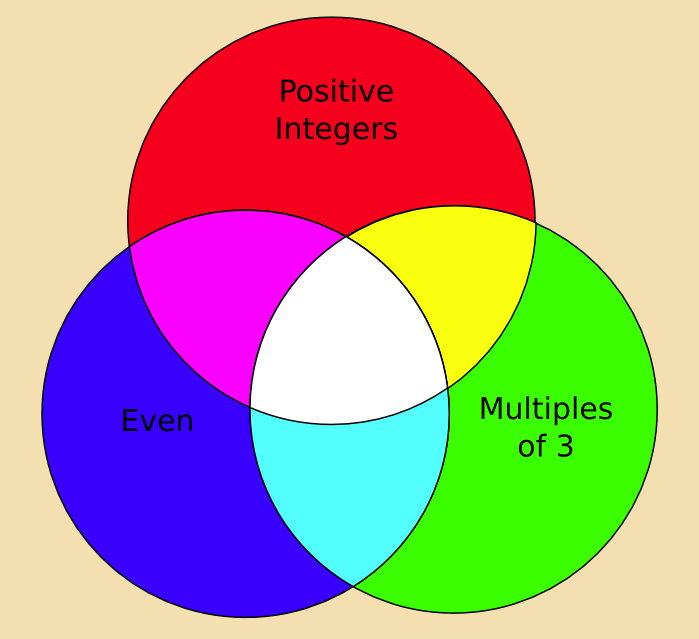
The positions of the three circles tell us information about what each set includes. The set labeled Even is partially inside of the set of Positive Integers because Positive Integers includes some Even, such as 8 or 26; however, Positive Integers also includes many numbers that are not even, such as 13 or 9,174,823, so part of the set Positive Integers is outside the set of Even. Likewise, Even includes many numbers that are not Positive Integers, such as -4 and -192, so part of the set Even is outside of the set Positive Integers.

The set labeled Multiples of 3 also intersects with the set Positive Integers because Positive Integers includes many Multiples of 3, such as 9 or 27; however, Positive Integers also includes many numbers that are not Multiples of 3, such as 1 or 17, so part of the set of Positive Integers is outside of the set Multiples of 3. Likewise, there are numbers which are Multiples of 3 that are not contained within the set Positive Integers, such as -6 or -87,630, so part of the set Multiples of 3 is outside of the set Positive Integers.

The sets labeled Even and Multiples of 3 intersect because some Even are Multiples of 3, and vice versa. A number like -6 would go in the intersection between Even and Multiples of 3 because it is both even and divisible by 3.

All three areas intersect in the center of the diagram. This area holds all numbers that are (a) Even, (b) Divisible by 3, and (c) Positive, such as 6 or 12.

Finally, outside of all the circles lies everything else. This space technically includes the universe and everything in it, from numbers not contained in any category (-5, -19) to imaginary numbers (3 i ) and even non-numerical sets of data (letters, song titles, etc). Anything that is not an integer that is positive, even, and/or divisible by 3 is considered to lie outside of the Venn Diagram.

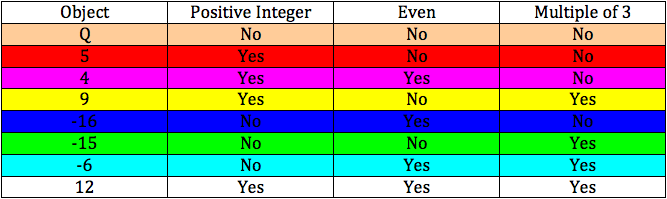
The following table gives examples of numbers that would go in each of the categories. The color of the number corresponds to that category's color in the Venn Diagram.

Related Resources

• Activity Bar Graph Sorter
• Activity Venn Diagram Shape Sorter
• Activity Venn Diagrams
• Discussion about Algorithm
• Discussion about Sets
• Discussion about Sets (Beginner)
• Discussion about Venn Diagram Beginner
• Discussion about Venn Diagrams
• Worksheet Triple Venn Diagram Shape Sorter Exploration Questions
• Worksheet Triple Venn Diagram Shape Sorter Exploration Questions (doc)
• Worksheet Venn Diagram Algorithm Worksheet
• Worksheet Venn Diagram Algorithm Worksheet (doc)
• Worksheet Worksheet for Sets and the Venn Diagram Beginner
• Worksheet Worksheet for Sets and the Venn Diagram Beginner (doc)

Controls and Output

There are two ways to play this activity. You can choose to Make the rules or Guess the rules.

Description

This activity allows the user to explore Venn Diagrams with three circles. Students can sort shapes into known categories or can guess what the categories are by experimenting with sorting. This activity would work well in groups of two for twenty to thirty minutes if you use the exploration questions and ten to fifteen otherwise.

Place in Mathematics Curriculum

This activity can be used to:

• introduce the concept of Venn Diagrams
• explore different types of diagrams
• develop logical thinking
• use Venn Diagrams as a tool for describing relationships in various academic subjects

Be Prepared to

• explain why some objects don't fall under the categories of any of the circles
• help students figure out how to guess the rule without placing every shape in the diagram

Related Resources

• Activity Bar Graph Sorter
• Activity Venn Diagram Shape Sorter
• Activity Venn Diagrams
• Discussion about Algorithm
• Discussion about Sets
• Discussion about Sets (Beginner)
• Discussion about Venn Diagram Beginner
• Discussion about Venn Diagrams
• Lesson on Algorithm Discovery with Venn Diagrams
• Lesson on Sets and the Venn Diagram
• Lesson on Sets and The Venn Diagram (Beginner)
• Lesson on Venn Diagrams
• Worksheet Triple Venn Diagram Shape Sorter Exploration Questions
• Worksheet Triple Venn Diagram Shape Sorter Exploration Questions (doc)
• Worksheet Venn Diagram Algorithm Worksheet
• Worksheet Venn Diagram Algorithm Worksheet (doc)
• Worksheet Worksheet for Sets and the Venn Diagram Beginner
• Worksheet Worksheet for Sets and the Venn Diagram Beginner (doc)