Linear Inequalities

What is Linear Inequalities?

What is an inequality?

This activity allows the user to graph linear inequalities in 2 variables. Users can input inequalities in algebraic form and graph them on a coordinate plane. The user can graph up to four inequalities as well as many ordered pairs. This activity is an extension of the Graphit applet.

Being able to graph inequalities is important in higher mathematics such as calculus and in areas that use mathematics such as physics.

In this activity, users will input values to create linear inequalities to be graphed. Rather then a straight line appearing as with linear functions, however, the inequality functions will have an area shaded above or below either a dotted or solid line (depending on the chosen inequality). This happens because the x and y values are not fixed (unless the = sign is chosen) and therefore there are many different values that they could exist for the function.

Let's take a look at one example of an inequality: 2X + 2Y LESS THAN 8

When this inequality is graphed, a dotted diagonal line crosses the points (0, 4) and (4, 0) with the area to the left of the line entirely shaded. This occurs because all of the shaded area represents possible values for the function. Let's see how this is done and choose a value for X.

If X = 0 then what are the possible values of Y?

2(0) + 2(Y) LESS THAN 8 0 + 2(Y) LESS THAN 8

Y LESS THAN 4

Therefore, when X=0, all values for Y below 4 could exist and therefore all values below are shaded. There is a dotted line because Y cannot equal 4. While this only shows what Y can be if X is 0, you can also experiment with different values of X (or Y) to find other possible values.

Related Resources

• Activity Data Flyer
• Activity Graphit
• Discussion about Gathering Information from Graphs
• Discussion about Inequalities
• Discussion about Linear Functions
• Worksheet Four Quadrant Grid, 14x18
• Worksheet Four Quadrant Grid, 28x36
• Worksheet Linear Inequalities Exploration Questions
• Worksheet Linear Inequalities Exploration Questions (doc)

How Do I Use This Activity?

This activity allows the user to plot ordered pairs and algebraic relations on the same coordinate plane.

Controls and Output

• The area at the top of the screen is where the plot is displayed.
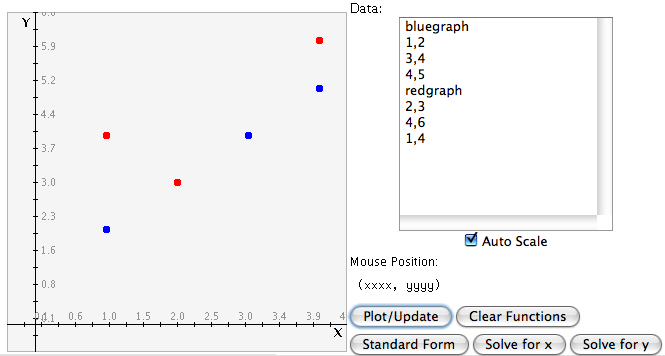
• The Relation and Data areas are for entering inequalities and ordered pairs, respectively. When entering an inequality first enter a value in the box before x and a value in the box before y. Next, select the inequality sign (less than, less than or equal to, equal to, greater than or equal to, or greater than). Lastly, enter a value in the last box. All values must be written as whole numbers or decimal values (not fractions). Once all of the boxes have values in them and the sign has been chosen, select the "Plot/Update" button and the data will appear on the graph. For information about entering data points, see Simple Plot.

• Once you have created an inequality relation, you can choose several ways to view the relation. By selecting the button "standard form" you will see the inequality written as you typed it in. For example: 2x + 3y LESS THAN 5. By selecting the button "solve for x" you will see the inequality written such that the inequality is solved in terms of x. For example, x LESS THAN -3/2y + 5/2. By selecting the button "solve for y" you will see the inequality written such that the inequality is solved in terms of y. For example, y LESS THAN -2/3x + 5/3.

  

• By selecting "Clear Relations" you can erase all values in the relations section, while keeping the data sets.

  

• You can plot a total of four relations and infinitely many data sets at once. Separate data sets by typing newgraph or by writing each data set on a line by itself in the Data window. If you want to specify your own colors for the graphs you can replace newgraph with the following keywords: bluegraph, redgraph, greengraph, darkbluegraph, graygraph, magentagraph, purplegraph, crimsongraph and then all of the values following that keyword will turn the corresponding color.

  

• You can choose from two plot types. "Connected" draws a line from one point to the next (before the line is drawn the points are sorted by their x coordinates.) "Scatter Plot" just draws the points as dots on the graph. These options do not affect the way relations are graphed. By selecting "Clear Data" you can erase all data sets, while keeping values in the functions section.

  

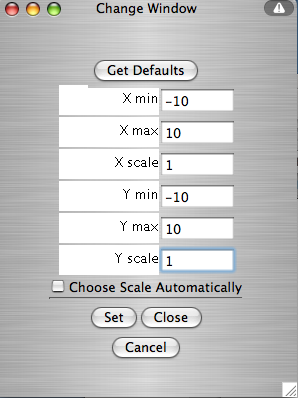
• The Set Window button brings up a separate window where you can determine how the coordinate plane will appear on your screen. X min and X max are the minimum and maximum x-values displayed on the graph. Similarly for Y min and Y max. X scale is the distance between vertical gridlines. Y scale is the distance between horizontal gridlines. If the Choose Scale Automatically box is checked, the applet will choose appropriate values for you to display all your data. If you uncheck that box, you override the auto scale values with your own. Any changes you make to the window parameters will take effect once you select the Set button.

  

• You can choose what you see on the graph. You can select to show all relations, all data, and/or the grid lines by checking the appropriate box or radio button in the Show section.

  

• The applet also can tell you the location of any click. Just click the mouse anywhere on the graph that you want to know the coordinates of and the coordinates will appear under the words Mouse Position:

  

Description

This activity allows the user to plot ordered pairs and linear inequality relations on the same coordinate plane. This activity would work well in groups of two to four for about forty-five minutes if you use the exploration questions and twenty minutes otherwise.

Place in Mathematics Curriculum

This activity can be used to:

• illustrate inequalities on the Cartesian coordinate system
• practice students' pattern recognition skills
• practice students' graph reading skills
• illustrate the relationship between graphical and algebraic representations of functions

Be Prepared to

• answer the question "Why are the areas shaded below/above the line?"
• answer the question "Why are some of my lines solid and others dashed?"
• discuss the concepts of multiple outputs for a single function
• discuss a solution set for multiple inequalities

Related Resources

• Activity Data Flyer
• Activity Graphit
• Discussion about Gathering Information from Graphs
• Discussion about Inequalities
• Discussion about Linear Functions
• Lesson on Graphs and Functions
• Lesson on More Complicated Functions: Introduction to Linear Functions
• Worksheet Four Quadrant Grid, 14x18
• Worksheet Four Quadrant Grid, 28x36
• Worksheet Linear Inequalities Exploration Questions
• Worksheet Linear Inequalities Exploration Questions (doc)