Overlapping Gaussians

What is Overlapping Gaussians?

Gaussian curves are used frequently when calculating probabilities of random events. A special type of Gaussian curve is the normal distribution which is useful in probability because the area under the curve is 1. Scientists often encounter data sets that can be represented by Gaussian curves. Whenever continuous measurements are taken, such as the height of plants, weight of humans, or pH of a mixture, a Gaussian distribution can usually represent the data. And as the number of data points increases, they will look more and more like a Gaussian curve.

In the case of weight of humans, if we take a sample of men or women of a certain height, there will be a lot of subjects that hover around the mean weight. Then as you get further away from that mean, you will notice fewer and fewer data points with the given weight.

This activity allows the user to view two Gaussian curves in the same window in order to analyze the possibility of a difference in two data sets. If the areas under the two curves occupy a similar area then there is statistical reason to believe that they might actually have the same mean despite a difference in the experimental mean.

The small differences in means that are examined might be due to the difference in theoretical probability verses experimental probability. When a random sample of a population is taken, it might not reflect the exact parameters of the entire population. This applet could be used to determine the probability that a random sample is actually indicative of its population.

Related Resources

• Activity Fitted Normal Distribution
• Activity Multi-Function Data Flyer
• Activity Normal Distribution
• Activity Skew Distribution
• Worksheet Overlapping Gaussians Exploration Questions
• Worksheet Overlapping Gaussians Exploration Questions (doc)

Controls and Output

Slider Bars

• Since the functions are already graphed, you may manipulate the coefficients and constants of the function with sliders. Manipulating the slider will result in manipulating the graph in different ways depending on the color of the slider.
  • Purple Slider: Adjusts the amplitude or height of the curve. The larger the value of the purple slider, the taller the function will be. This value should always be greater than zero.
  • Red Slider: Adjusts the standard deviation or width of the curve. As this value increases, the graph will appear to stretch out horizontally. This value should always be greater than zero.
  • Green Slider: Adjusts the mean or horizontal shift of the curve. As you adjust this slider, the graph will slide horizontally. This variable can take on any value.
  
  
• After changing the function with the sliders, you may set the sliders back to the original values when the function was entered by clicking the Reset Sliders button.
  
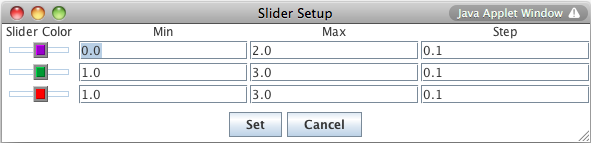
• You may manipulate the maximum, minimum, and increment of each slider bar. The Slider Limits button brings up a dialog box that allows you to set the minimum and maximum values of each slider bar, as well as the step size for each adjustment of the slider. The step size determines how precisely you can control the value of the constant. For instance, if you set the minimum to 0, the maximum to 1, and the step to 0.1, moving the slider will step the constant from 0 to 0.1 to 0.2, and so on. However, if you set the step to 0.2, the slider will step the constant from 0 to 0.2, 0.4, etc.
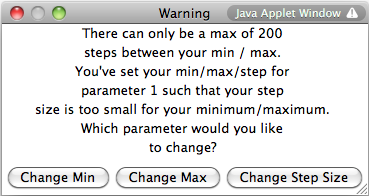
• The number of steps between the slider minimum and maximum must be smaller than 200. If you enter parameters such that the number of steps is greater than 200, then an error message appears asking you to readjust by changing the slider min, slider max, or step size.
  

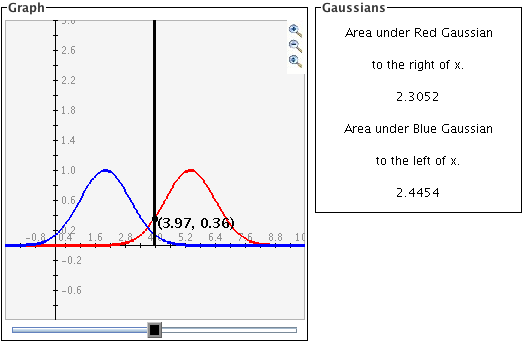
• The black slider bar sets a bound for integrals of the two Gaussian curves. For the red curve, the black slider sets the lower bound for the integral with the upper bound being infinity. For the blue curve, it sets the upper bound for the integral with the lower bound being negative infinity. The results of these integrals are displayed in the box labeled Gaussians.
  

• There are three types of grids: No Grid, Light Grid Lines, and Dark Grid Lines. To activate any of these three options, highlight the circle next to the appropriate option:

No Grid Lines	Light Grid Lines	Dark Grid Lines

• Setting exact values for axis minimums and maximums: You may set the graph boundaries by clicking the Set Window button and entering new values for the x max, x min, y max, or y min. You can also set how the x and y scales increment or you can choose to have the activity choose these values automatically. Click the Set Window button to set the values.
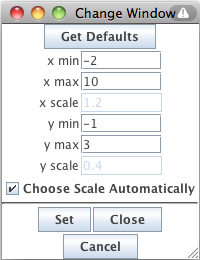  To return the values to their defaults, click the Get Defaults button and then click the Set button again. If you do not want to change the window settings you may click Cancel.
• Zoom/Pan buttons. In the upper right corner of the graph, there are three buttons with pictures of magnifying glasses. From top to bottom these buttons represent zoom in, zoom out, and pan, respectively.
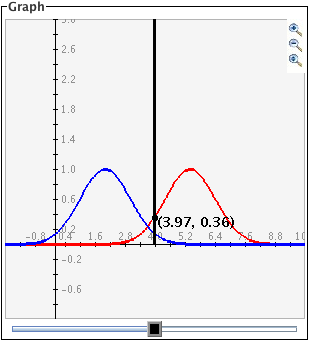
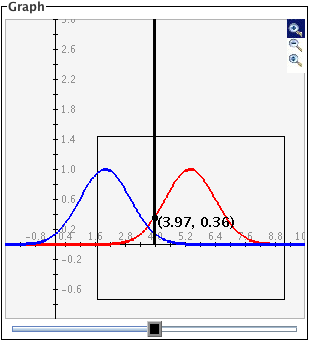
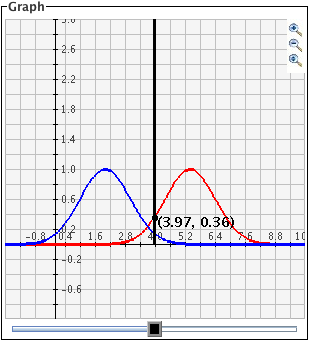
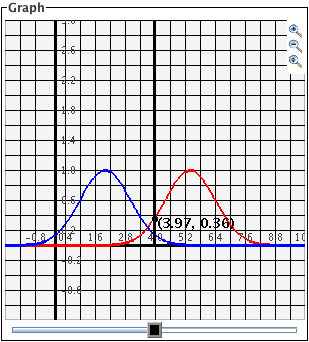
  • To zoom in, click the top button to depress it, then click and drag over the area of the graph that you wish to magnify. The images below show first the process of dragging a box around a desired zoom area with the mouse (left), and then the resulting zoomed image after the mouse button is released (right). Note that after the zoom-in has been performed, the zoom-in button at top right is no longer depressed.
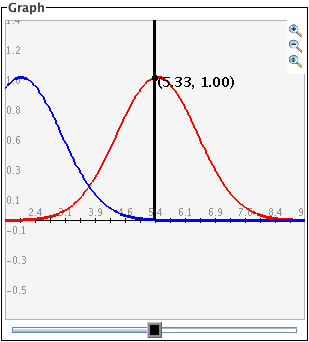
  • To zoom out, simply click the second of the three zoom buttons. The graph will automatically zoom out by doubling the min and max values of the axes.
  • To pan, click the bottom magnifying glass button to depress it. Click and drag over the graph and the graph will pan around according to the movement of the mouse. Upon releasing the mouse, the pan button is released.

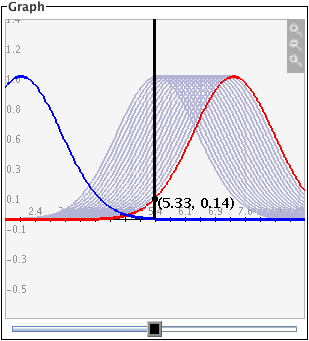
• Checking the Show Trace box will cause old graph lines to remain visible (in a lighter gray) as you change the function by moving the sliders. To remove the trace, click the Clear Trace button. To stop the tracing, uncheck the Show Trace check box.

Description

The Overlapping Gaussian applet is designed to allow the user to shift the parameters on two Gaussian curves and then determine whether a difference in the data sets represented by the curves is likely to exist or not. This activity measures the area under the Gaussian curves, which is a tool used to calculate probabilities in normally distributed data.

This activity would work well for individuals or in groups of two to three for about twenty-five to thirty-five minutes if you use the exploration questions.

Place in Mathematics Curriculum

This activity can be used to:

• Calculate P-values for normal curves
• Teach students how changing different parameters affects a Gaussian curve
• Teach students how the area under a Gaussian curve relates to probability
• Introduce students to Type I and Type II errors

Be Prepared to

• Explain Gaussian/Normal Curves
• Explain Mean/Standard Deviation
• Explain how P-values are calculated
• Introduce Type I/Type II errors

Related Resources

• Activity Fitted Normal Distribution
• Activity Multi-Function Data Flyer
• Activity Normal Distribution
• Activity Skew Distribution
• Worksheet Overlapping Gaussians Exploration Questions
• Worksheet Overlapping Gaussians Exploration Questions (doc)