Slope Slider

What is Slope Slider?

This activity allows the user to explore the relationship between slope and intercept in the Cartesian coordinate system.

The applet allows the manipulation of a linear function. The user may view the function in two forms: slope-intercept form, f(x) = mx + b, or standard notation, ax + by = c. There is a slider to change each coefficient and constant, so the user can manipulate the line and a point along the line.

Related Resources

• Activity Conic Flyer
• Activity Data Flyer
• Activity Function Flyer
• Activity Graph Sketcher
• Activity Graphit
• Activity Simple Plot
• Discussion about From Graphs to Function Machines and Back
• Discussion about Gathering Information from Graphs
• Discussion about Introduction to the Coordinate Plane and Coordinates
• Discussion about Linear Functions
• Discussion about Slope and Y-intercept
• Worksheet Slope Slider Exploration Questions
• Worksheet Slope Slider Exploration Questions (doc)
• Worksheet Slope Slider Record Sheet
• Worksheet Slope Slider Record Sheet(large)

How Do I Use This Activity?

This activity allows the user to use various controls to manipulate a linear function graphically.

Controls and Output

• There is a graph at the top of the activity. Below the graph are various slider bars. Moving the black slider bar left or right with the mouse permits the user to change the location of the point along the line.
• When the equation of the line is in slope-intercept form, the purple slider allows the user to manipulate the slope of the line. The green slider allows the user to manipulate the y-intercept of the line. Note how the function and the graph change when you manipulate the slope and y-intercept sliders.
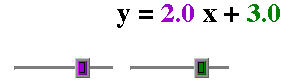
• You can also view the equation in Standard Notation by checking the Standard Notation checkbox.
• Doing so will enable a third slider bar. The purple and green sliders affect the slope of the line. The green and blue sliders affect the y-intercept of the line. The purple and blue sliders affect the x-intercept of the line. Note how the line changes when you manipulate these sliders compared to when the line is in slope-intercept form.
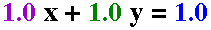
• While in standard notation (Ax+By=C), if A=0 and B=0, the black slider bar will be disabled and the graph will be empty because the equation is unsolvable for all values of C. Given A=0, B=0, and C=0, all values of x and y satisfy the equation so there is no unique solution. Given A=0, B=0, and C≠0, no values of x and y satisfy the equation so there is no solution.
  
  
• While in standard notation (Ax+By=C), if B=0, A≠0, and C≠0, the black slider bar will be disabled, but a vertical line will still appear on the graph. Given these parameters, the purple and blue sliders will only affect the x-intercept of the line since it is vertical.
  
  
• The Link Sliders check box, when activated, allows the user to move both sliders simultaneously provided both sliders may be moved in the direction of the dragged slider. For example, if Link Sliders is checked and the purple slider is moved five units to the right, the green slider will also move five units to the right provided there is space for the green slider to do so.
• The Show Trace check box, when activated, allows the user to see the various intermediate stages as the line changes in response to changes in the slider bars.
• By clicking the Clear Trace button, the user can clear the traces that are left on the graph after using the Show Trace feature.
• The two radio buttons on the bottom of the activity control whether decimals or fractions are used for the numbers. For instance, if you select Use Decimals, one tenth will be represented as 0.1. If you select Use Fractions, one tenth will be represented as 1/10.
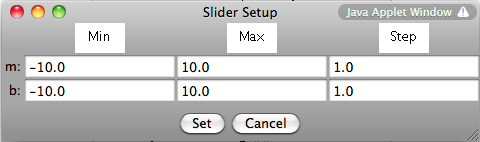
• The Slider Settings button brings up a dialog box that allows you to set the minimum and maximum values of each slider bar. You can also set the step size for each slider bar. The step size controls the size of the increment for the values on a slider bar. For instance, if you set the minimum to 0, the maximum to 1, and the step to 0.1, the slider will increment the value of the constant at the intervals of 0, 0.1, 0.2, etc. However, if you set the step to 0.2, the slider will stop at 0, 0.2, 0.4, etc. The input will always be rounded to the nearest tenth when using decimal values.

  The number of increments must be smaller than 100. If you enter parameters such that the number of steps is greater than 100 then an error message appears asking you to readjust by setting the slider min, slider max, or step size.

  

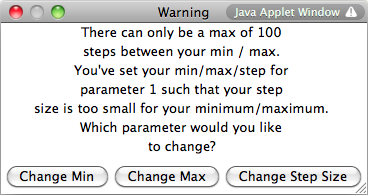
  For example, suppose you are using fractions and you want a step size of 1/8 for m. The default min/max of -10 to 10 with a step size of 1/8 would result in 160 steps which would generate the Warning window. Suppose you select change min. The new Slider Setup would calculate an appropriate min (reduced to lowest terms) that would allow 100 steps of size 1/8 between the new min and the original max. The appropriate slider would be recalibrated and the values of m would appear as fractions reduced to lowest terms.

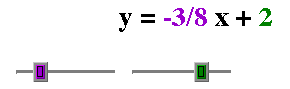
• There are three types of grids: No Grid, Light Grid Lines, and Dark Grid Lines. To activate any of these three options, highlight the circle next to the appropriate option:

  No Grid graph:	Light Grid Line graph:	Dark Grid Grid Line graph:

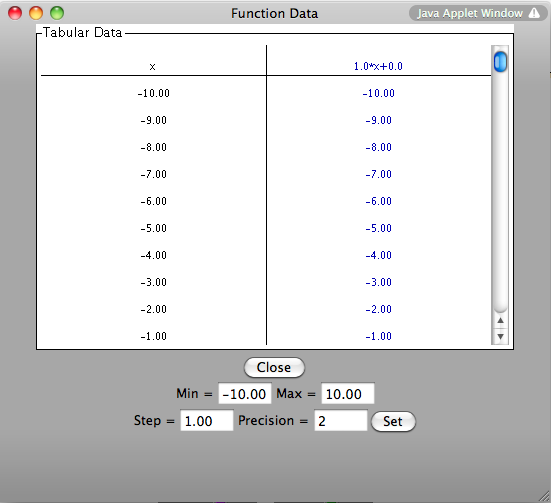
• To view a table of values corresponding to the graphed function, click the Show Tabular Data button.
• The x values in the table increment equally and then give the corresponding f(x) values for the function. You can change these data values by entering a new minimum x value, new maximum x value, and step size. If you enter a step that does not divide evenly into the range, the table will stop at the greatest multiple of the step that is less than the maximum. The precision field allows you to adjust the number of decimal points to print out values of x and f(x).

Description

This activity allows the user to experiment with slope and y-intercept. This activity would work well in groups of two to four for about thirty to forty-five minutes if you use the exploration questions and fifteen to twenty minutes otherwise.

Place in Mathematics Curriculum

This activity can be used to:

• introduce slope-intercept form of a line
• introduce slope and y-intercept

Be Prepared to

• answer the question "Which is the x-axis and which is the y-axis?"
• discuss slope, intercepts, and functions

Related Resources

• Activity Conic Flyer
• Activity Data Flyer
• Activity Function Flyer
• Activity Graph Sketcher
• Activity Graphit
• Activity Simple Plot
• Discussion about From Graphs to Function Machines and Back
• Discussion about Gathering Information from Graphs
• Discussion about Introduction to the Coordinate Plane and Coordinates
• Discussion about Linear Functions
• Discussion about Slope and Y-intercept
• Lesson on Cartesian Coordinate System
• Lesson on Graphs and Functions
• Lesson on Introduction to Functions
• Worksheet Slope Slider Exploration Questions
• Worksheet Slope Slider Exploration Questions (doc)
• Worksheet Slope Slider Record Sheet
• Worksheet Slope Slider Record Sheet(large)