What is Function Flyer?
This activity works like a graphing calculator. After entering the function, the user can view a graph of the function where y = f(x). Beneath the graph are slider bars that allow the user to manipulate the graph by changing the values of exponents, coefficients, and constants.
This activity allows the user to explore the effect of changing constants in most types of functions including:
- linear
- quadratic
- exponential
- trigonometric
How Do I Use This Activity?
This activity allows the user to graph an algebraic function on a coordinate plane with the ability to use sliders to manipulate the constants of the graphed function.
Controls and Output
Find out how to...
| Add Grid Lines | Change X min/max and Y min/max | Graph Functions | Show Tabular Function Data |
| Show Asymptotes | Trace Function | Sliders |
The area in the center of the screen is where the plot is displayed.
-
There are three types of grids:
No Grid,
Light Grid Lines, and
Dark Grid Lines. To activate any of these three options, highlight the circle next to the appropriate
option:

No Grid graph: Light Grid Line graph: Dark Grid Grid Line graph: 
-
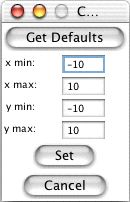
Setting exact values for axis mins/maxes: You may set the graph boundaries by clicking the Set Window button and entering new values for the x max, x min, y max, or y min. Then click the Set button to set the boundaries. To return the values to their defaults, you click the Get Defaults button and then click the Set button again. If you do not want to change the window settings you may click Cancel.
-
Zoom/Pan buttons: In the upper right corner of the graph, there are three buttons with pictures of magnifying
glasses. From top to bottom these buttons represent zoom in, zoom out, and pan,
respectively.
-
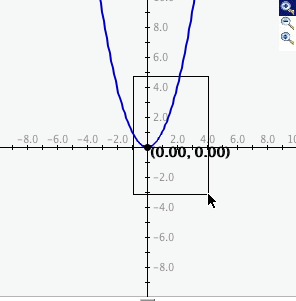
To zoom in, click the top button to depress it, then click and drag over the area of the
graph that you wish to magnify. The images below show first the process of dragging a
box around a desired zoom area with the mouse (left), and then the resulting zoomed
image after the mouse button is released (right). Note that after the zoom-in has been
performed, the zoom-in button at top right is no longer depressed.
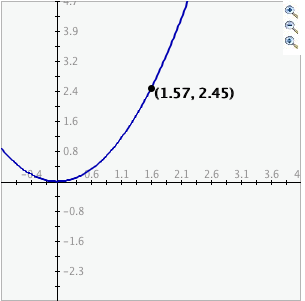
- To zoom out, simply click the second of the three zoom buttons. The graph will automatically zoom out by doubling the min and max values of the axes.
- To use the pan feature, click the bottom magnifying glass button to depress it. Click and drag over the graph and the graph will pan around according to the movement of the mouse. Upon releasing the mouse, the pan button is released.
-
To zoom in, click the top button to depress it, then click and drag over the area of the
graph that you wish to magnify. The images below show first the process of dragging a
box around a desired zoom area with the mouse (left), and then the resulting zoomed
image after the mouse button is released (right). Note that after the zoom-in has been
performed, the zoom-in button at top right is no longer depressed.
-
Checking the
Show Trace button will cause old graph lines to remain visible (in a lighter color) as you change the
function by moving the sliders. To remove all the old lines, click the
Clear Trace button. To stop tracing, uncheck the
Show Trace check box.

- When Show Trace is checked, you will be unable to Plot Data, Show Squares, Auto Scale, Show Vertical Asymptotes, use the pan/zoom features, or change the darkness of the grids. When any of these options are checked, you will be unable to Show Trace.
-
You may see the vertical asymptotes of a graph (if there are any) by checking the
Show Vertical Asymptotes check box. For example, the tangent graph with this option selected looks like:
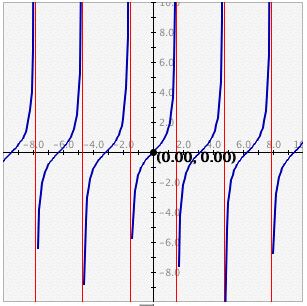
* Note that due to the programming technique used to detect asymptotes, this program will only detect those asymptotes that go from a large positive y value to a large negative y value at the discontinuity. f(x)=log(x) is an example of a vertical asymptote Data Flyer will not detect.
- Function Flyer allows you to enter an algebraic function in the box labeled f(x)= . For information on the syntax of entering functions and numbers with scientific notation, see Interactivate Functions Help.
- Note that numerical values entered should be accurately calculated from 10 -8 to 10 8 . Numbers larger or smaller than these values produce unreliable results. If you enter a number with a magnitude smaller than 10^-6 or larger than 10^6 it will automatically be converted to scientific notation.
-
Enter the function you want to graph in the box marked
f(x)=. Any constant or coefficient you wish to manipulate must be entered as a number. For
instance, if you wish to experiment with the linear function f(x) = x + 8 and wish to
manipulate the coefficient of x it is necessary to type the equation as f(x) = 1*x + 8 so
the computer recognizes the multiplier as a parameter. Likewise if you want to experiment
with the sine function f(x) = sin(x) and be able to manipulate the parameters such as the
y-intercept, phase, frequency, and amplitude, it is necessary to type 1*sin(1*x+0)+0. (Try
typing in both and clicking the set function button so you can see the difference.)

-
Once you have set the function you may enter a different function by clicking the Change Function button, entering the new function, and clicking the Set Function button again.

-
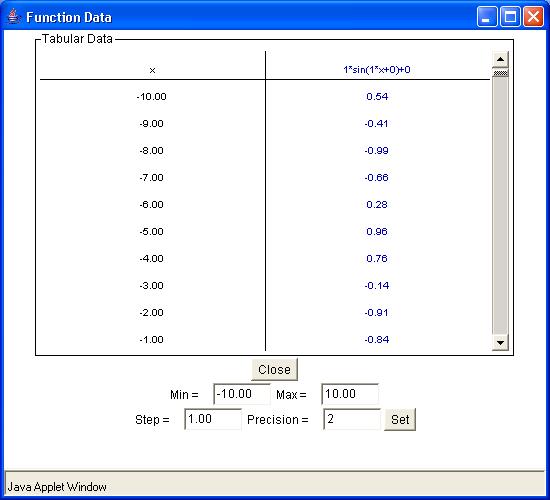
To view a table of values corresponding to the graphed function, click the
Show Tablular Data button.

-
The x values in the table increment equally and then give the corresponding f(x) values
for the function. You can change these data values by entering a new minimum x value, new
maximum x value, and step size. If you enter a step that does not divide evenly into the
range, the table will stop at the greatest multiple of the step that is less than the
maximum. The precision field allows you to adjust the number of decimal places to print
out the values of x and f(x).
-
You may set the sliders back to the original values that they had when the the function
was entered by clicking the
Reset Sliders button.

-
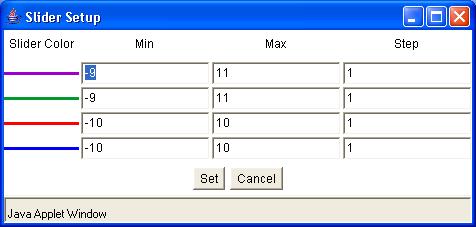
The
Slider Limits button brings up a dialog box that allows you to set the minimum and maximum values of
each slider bar. You can also set the step size for each slider bar. The step size
determines how precisely you can control the value of the constant. For instance, if you
set the minimum to 0, the maximum to 1, and the step to 0.1, moving the slider will step
the constant from 0 to 0.1 to 0.2, and so on. However, if you set the step to 0.2, the
slider will step the constant to 0, 0.2, 0.4, etc.
-
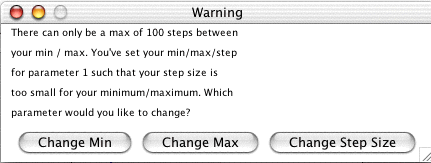
The number of increments must be smaller than 100. If you enter parameters such that the
number of increments is greater than 100, then an error message appears asking you to
re-adjust by changing the slider min, slider max, or step size.
-
Checking the
Exponents Change box before clicking
Set Function will allow you, after the function is graphed, to use slider bars to adjust the values of
any exponents.

Description
This activity allows the user to experiment with changing constants and coefficients in a function. This activity would work well in groups of two to four for about fifteen minutes per function type with the exploration questions and ten minutes per function type otherwise..
Place in Mathematics Curriculum
This activity can be used to:
- experiment on the graph of a function by changing the coefficients and constants in a given type of function.
Standards Addressed
Grade 9
-
Functions and Relationships
- The student demonstrates conceptual understanding of functions, patterns, or sequences including those represented in real-world situations.
- The student demonstrates algebraic thinking.
Grade 10
-
Functions and Relationships
- The student demonstrates conceptual understanding of functions, patterns, or sequences including those represented in real-world situations.
- The student demonstrates algebraic thinking.
Eighth Grade
-
Functions
- Define, evaluate, and compare functions.
- Use functions to model relationships between quantities.
Algebra
-
Arithmetic with Polynomials and Rational Expressions
- Perform arithmetic operations on polynomials
-
Seeing Structure in Expressions
- Interpret the structure of expressions
Functions
-
Building Functions
- Build a function that models a relationship between two quantities
- Build new functions from existing functions
-
Interpreting Functions
- Understand the concept of a function and use function notation
- Interpret functions that arise in applications in terms of the context
- Analyze functions using different representations
-
Linear, Quadratic, and Exponential Models
- Construct and compare linear, quadratic, and exponential models and solve problems
- Interpret expressions for functions in terms of the situation they model
-
Trigonometric Functions
- Model periodic phenomena with trigonometric functions
Grades 6-8
-
Algebra
- Represent and analyze mathematical situations and structures using algebraic symbols
- Understand patterns, relations, and functions
Grades 9-12
-
Algebra
- Analyze change in various contexts
- Represent and analyze mathematical situations and structures using algebraic symbols
- Understand patterns, relations, and functions
- Use mathematical models to represent and understand quantitative relationships
Algebra II
-
Algebra
- Competency Goal 2: The learner will use relations and functions to solve problems.
Advanced Functions and Modeling
-
Algebra
- Competency Goal 2: The learner will use functions to solve problems.
Pre-Calculus
-
Geometry and Measurement
- Competency Goal 2: The learner will use relations and functions to solve problems.
-
Number and Operations
- Competency Goal 1: The learner will describe geometric figures in the coordinate plane algebraically.
Integrated Mathematics III
-
Algebra
- Competency Goal 3: The learner will use relations and functions to solve problems.
Integrated Mathematics IV
-
Algebra
- Competency Goal 4: The learner will use relations and functions to solve problems.
AP Calculus
-
Numbers and Operations
- Competency Goal 1: The learner will demonstrate an understanding of the behavior of functions.
Algebra I
-
Foundation for Functions
- 1. The student understands that a function represents a dependence of one quantity on another and can be described in a variety of ways.
- 2. The student uses the properties and attributes of functions.
- 3. The student understands how algebra can be used to express generalizations and recognizes and uses the power of symbols to represent situations.
-
Linear Functions
- 5. The student understands that linear functions can be represented in different ways and translates among their various representations.
- 6. The student understands the meaning of the slope and intercepts of the graphs of linear functions and zeros of linear functions and interprets and describes the effects of changes in parameters of linear functions in real-world and mathematical situations.
-
Quadratic and Other Nonlinear Functions
- 9. The student understands that the graphs of quadratic functions are affected by the parameters of the function and can interpret and describe the effects of changes in the parameters of quadratic functions.
- 11. The student understands there are situations modeled by functions that are neither linear nor quadratic and models the situations.
Textbooks Aligned
Grade Seven
-
Accentuate the Negative
- Investigation Five: Coordinate Grids
-
Comparing and Scaling
- Investigation Four: Comparing By Finding Rates
-
Moving Straight Ahead
- Investigation One: Predicting from Patterns
- Investigation Two: Walking Rates
- Investigation Four: Solving Equations
- Investigation Five: Exploring Slope
-
Variables and Patterns
- Investigation One: Variables and Coordinate Graphs
- Investigation Two: Graphing Change
- Investigation Three: Analyzing Graphs and Tables
Grade Eight
-
Frogs, Fleas and Painted Cubes
- Investigation One: Introduction to Quadratic Relationships
- Investigation Two: Quadratic Expressions
- Investigation Three: Quadratic Patterns of Change
- Investigation Four: What Is a Quadratic Function?
- Investigation Five: Painted Cubes
-
Growing, Growing, Growing
- Investigation One: Exponential Growth
- Investigation Two: Growth Patterns
- Investigation Three: Growth Factors
- Investigation Four: Exponential Decay
-
Samples and Populations
- Investigation One: Comparing Data Sets
-
Thinking with Mathematical Models
- Investigation One: Linear Models
- Investigation Two: Nonlinear Models
- Investigation Three: More Nonlinear Models
- Investigation Four: A World of Patterns
Book 1
-
Module 3 - Statistical Safari
- Section 3: Line Plots
Book 2
-
Module 2 - Search and Rescue
- Section 4: Graphing Functions
-
Module 7 - Health and Wellness
- Section 1: Formulas and Graphs
Book 3
-
Module 3 - The Mystery of Blacktail Canyon
- Section 2: Graphing Equations
- Section 3: Slopes
-
Module 7 - Visualizing Change
- Section 5: Parabolas
- Section 5: Quadratic Equations
8th
-
Module 6 - Visualizing Change
- Section 5: Exploring Quadratic Functions
Book 1
-
Patterns in Numbers and Shapes
- Lesson 7: Gridpoint Pictures
- Lesson 8: Points, Plots, and Patterns
- Lesson 9: Payday at Planet Adventure
- Lesson 12: The Will
-
What Does the Data Say?
- Lesson 7: Are You Improving?
- Lesson 8: How Close Can You Get?
- Lesson 9: Stories and Graphs
Book 2
-
Buyer Beware
- Lesson 2: The Best Snack Bar Bargain
-
Getting Down to Business
- Lesson 7: How Mant Sales at Tee-Time?
- Lesson 8: How Much Profit at Tee-Time?
- Lesson 9: Months Later at Tee-Time
-
The Language of Algebra
- Lesson 5: Seeing Things Graphically
- Lesson 6: The Algebra Walk
- Lesson 7: Putting It All Together
- Lesson 8: The Top-Selling Albums of All Time, Part 2
- Lesson 12: The Top-Selling Albums of All Time, Part 3
Book 3
-
Family Portraits
- Lesson 2: Keeping a Steady Pace
- Lesson 3: How Long Is a Meter
- Lesson 4: A New Slant on Linear Functions
- Lesson 7: The Area of a Projected Image
- Lesson 8: Going Around a Curve
- Lesson 9: Fenced In
- Lesson 10: Folds and Regions
- Lesson 11: Rules of the Road for Exponents
- Lesson 12: The Very Large and the Very Small
-
Looking Behind the Numbers
- Lesson 6: Is There a Relationship?
- Lesson 7: What Type of Relationship Is It?
- Lesson 8: The Mysterious Footprint
-
Mathematics of Motion
- Lesson 5: Walk This Way
- Lesson 6: Stories, Maps, and Graphs
- Lesson 7: A Graphing Matter
- Lesson 9: The Race Announcer
- Lesson 10: How Fast? How Far? How Long?
- Lesson 11: The Race Is On!
- Lesson 12: Final Project
-
Shapes and Space
- Lesson 4: Moving the Cube
-
What Comes Next?
- Lesson 8: Which Model Fits the Data Better?
- Lesson 9: Making Plans
- Lesson 10: Looking Ahead
Grade 8
-
Get the Most Out of It
- Word Problems with Two Unknowns
- Systems of Equations
- Graphing Lines
- Graphing Inequalities
- Graphing Hyperbolas
-
Graphing Equations
- Graphing Points and Lines
- Solving Linear Equations
- Graphing Inequalities
- Equation of a line
-
Growth
- Linear functions
- Quadratic Functions
- Cubic Functions
- Exponential Functions
- Sequences
- Growth
Grade 5
-
Figuring All the Angles
- Measuring Angles
- Vectors
- Rectangular Coordinates
- Polar Coordinates
-
Patterns and Symbols
- Variables
- Patterns
- Pattern Rule
-
Picturing Numbers
- Bar Graphs
- Line Graphs
- Pie Charts
- Pictographs
- Describing Data
- Using Data for Arguments
Grade 6
-
Dealing With Data
- Scatter Plots
- Box Plots
- Stem and Leaf Plot
- Histograms
- Mean, Median, Mode and Range
-
Operations
- Operations with Integers
- Plotting Points
- Coordinate Plane
-
Tracking Graphs
- Line Graphs
- Interpreting Graphs
- Looking at a Graph's global features
Grade 7
-
Packages and Polygons
- Geometric Shapes
- Models
- Properties of Regular and Semi-Regular Polyhedra
-
Ups and Downs
- Increasing and Decreasing Functions
- Linear Functions
- Periodic Functions
Be Prepared to
- answer the question "Which is the x-axis and which is the y-axis?"
- generalize the effects of changing the constants or coefficients in the type of function the students are studying