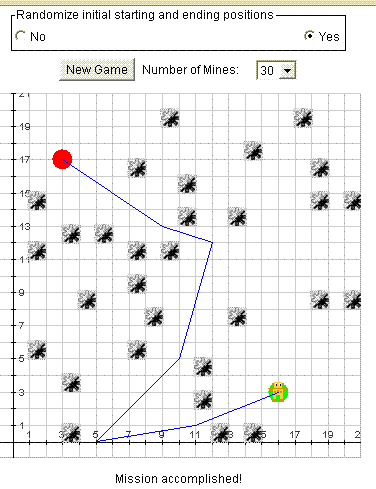
What is Simple Maze Game?
This game allows users to practice their point plotting skills by having them move a robot through a mine field to a target location. Moves are accomplished by specifying the coordinates of the new location. In order to win, the path must not cross a mine.
The coordinate plane system was developed by a sick mathematician. As Rene Descarte lay in bed sick, he saw a fly buzzing around on the ceiling. His ceiling was made of square tiles. As he watched, he realized that he could describe the position of the fly by the ceiling tile he was on. After this experience, he developed the Cartesian coordinate system in the 17th century to help visualize functions via plotting function values as ordered pairs. In this system a grid of evenly spaced horizontal and vertical lines is drawn, a center or "origin" is chosen, and horizontal and vertical scales are chosen. Here's an example:
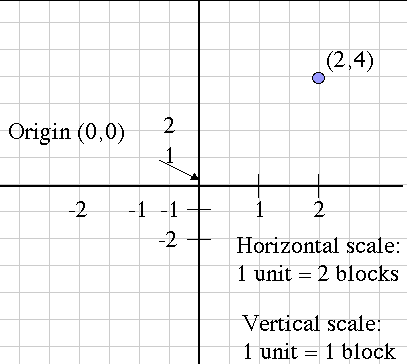
Notice that the blue point is labeled with its Cartesian coordinates, the horizontal and vertical movement from the origin, in that order. This is the mathematical convention for naming points.
Another name for the horizontal movement value is the abscissa, and the vertical movement is the ordinate. These terms are more rare now than they used to be, but you might still hear them being used.
How Do I Use This Activity?
This game allows users to practice their point plotting skills by having them move a robot through a mine field to a target location. Moves are accomplished by specifying the coordinates of the new location. In order to win, the path must not cross a mine.
Object of the Game The goal of the game is to guide the robot to the green dot. The robot moves by straight lines: horizontal, vertical, and diagonal. Each "step" starts from where the robot is, and ends at an intersection of grid lines chosen by user. In order to choose the end point of the next step, the user has to enter the coordinates of that point. The robot should avoid mines. Before making a step, it checks to see if there are any mines ahead. If there is a mine on the robot's path, it will explode as a result of the robot checking the path. The robot will not be harmed; it will not make a dangerous step. If a mine expoldes simply rethink the course you would like the robot to take and enter new coordinates.
Controls and Output
-
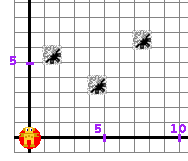
Determine the X and Y coordinates at the end point of the robot's next step. For example,
we want the robot to go to the right and up, but still avoid the mines. We could send him
over to the point X = 10 and Y = 3.
-
To command the robot to make the next step, type the X coordinate in the
X=[ ___ ] space, and the Y coordinate in the
Y=[ ___ ] space:
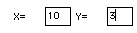
-
When coordinates for the next step are prepared, click on the
GO button to make the robot move. The movements of the robot are traced in blue:
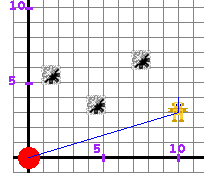
-
To start a new game, choose the
Number of Mines you want on the board:
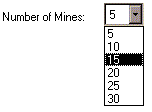 and click on the
New Game button:
and click on the
New Game button:

-
The user can control whether the robot starting and target positions are fixed or variable
using the following control:
If this control is set to No, the robot's starting position is always (0, 0) and the robot's target position is always (20, 20). If this control is set to Yes, the robot's starting and target position are placed at random positions on the screen as shown below:
Because this activity randomly generates questions, a feature called Seed Random has been implemented that allows multiple users using different computers to work on the same problem. See Seed Random Help for instructions on using this feature.
Description
This activity allows the user to practice their point plotting skills by having them move a robot through a mine field to a target location. Moves are accomplished by specifying the coordinates of the new location. In order to win, the path must not cross a mine. This activity would work well in groups of two for about fifteen minutes.
Place in Mathematics Curriculum
This activity can be used to:
- introduce the Cartesian coordinate system
- practice students' point plotting skills
- practice students' graph reading skills
- motivate the concept of slope
Standards Addressed
Grade 3
-
Geometry
- The student demonstrates understanding of position and direction.
Grade 4
-
Geometry
- The student demonstrates understanding of position and direction.
Grade 5
-
Geometry
- The student demonstrates understanding of position and direction.
Grade 6
-
Geometry
- The student demonstrates understanding of position and direction.
Grade 7
-
Geometry
- The student demonstrates understanding of position and direction.
Grade 8
-
Geometry
- The student demonstrates understanding of position and direction.
Grade 9
-
Geometry
- The student demonstrates understanding of position and direction when solving problems (including real-world situations).
Grade 10
-
Geometry
- The student demonstrates understanding of position and direction when solving problems (including real-world situations).
Grade 4
-
Measurement and Geometry
- 2.0 Students use two-dimensional coordinate grids to represent points and graph lines and simple figures
Fifth Grade
-
Geometry
- Graph points on the coordinate plane to solve real-world and mathematical problems.
Grades 3-5
-
Geometry
- Specify locations and describe spatial relationships using coordinate geometry and other representational systems
Grade 4
-
Number and Operations, Measurement, Geometry, Data Analysis and Probability, Algebra
- COMPETENCY GOAL 3: The learner will recognize and use geometric properties and relationships.
Grade 6
-
Number and Operations, Measurement, Geometry, Data Analysis and Probability, Algebra
- COMPETENCY GOAL 3: The learner will understand and use properties and relationships of geometric figures in the coordinate plane.
Grade 7
-
Number and Operations, Measurement, Geometry, Data Analysis and Probability, Algebra
- COMPETENCY GOAL 5: The learner will demonstrate an understanding of linear relations and fundamental algebraic concepts.
4th Grade
-
Geometry
- Standard 4-4: The student will demonstrate through the mathematical processes an understanding of the relationship between two- and three-dimensional shapes, the use of transformations to determine congruency, and the representation of location and moveme
- Standard 4-4: The student will demonstrate through the mathematical processes an understanding of the relationship between two- and three-dimensional shapes, the use of transformations to determine congruency, and the representation of location and movement within the first quadrant of a coordinate system.
Elementary Algebra
-
Elementary Algebra
- Standard EA-4: The student will demonstrate through the mathematical processes an understanding of the procedures for writing and solving linear equations and inequalities.
5th Grade
-
Geometry
- The student will develop an understanding of geometric concepts and relationships as the basis for geometric modeling and reasoning to solve problems involving one-, two-, and three-dimensional figures.
4th Grade
-
Geometry
- The student will develop an understanding of geometric concepts and relationships as the basis for geometric modeling and reasoning to solve problems involving one-, two-, and three-dimensional figures.
Grade 5
-
Geometry and Spatial Reasoning
- 9. The student recognizes the connection between ordered pairs of numbers and locations of points on a plane. The student is expected to locate and name points on a coordinate grid using ordered pairs of whole numbers.
Grade 6
-
Geometry and Spatial Reasoning
- 7. The student uses coordinate geometry to identify location in two dimensions. The student is expected to locate and name points on a coordinate plane using ordered pairs of non-negative rational numbers.
Grade 7
-
Geometry and Spatial Reasoning
- 7. The student uses coordinate geometry to describe location on a plane.
4th Grade
-
Geometry
- 4.15.b The student will describe the path of shortest distance between two points on a flat surface.
- 4.16 The student will identify and draw representations of lines that illustrate intersection, parallelism, and perpendicularity.
- 4.18 The student will identify the ordered pair for a point and locate the point for an ordered pair in the first quadrant of a coordinate plane.
-
Geomety
- 4.15.b
- 4.16
- 4.18
Be Prepared to
- answer the question "How do you find distance?"
- discuss distance, positive coordinates, integers etc